Paraboloid Quadric
Relevante Bilder
Relevante Artikel
QuadrikEine Quadrik ist in der Mathematik die Lösungsmenge einer quadratischen Gleichung mehrerer Unbekannter. In zwei Dimensionen bildet eine Quadrik im Regelfall eine Kurve in der Ebene, wobei es sich dann um einen Kegelschnitt handelt. In drei Dimensionen beschreibt eine Quadrik im Regelfall eine Fläche im Raum, die auch Fläche zweiter Ordnung oder quadratische Fläche genannt wird. Allgemein handelt es sich bei einer Quadrik um eine algebraische Varietät, also um eine spezielle Hyperfläche, in einem endlichdimensionalen reellen Koordinatenraum. Durch eine Hauptachsentransformation lässt sich jede Quadrik auf eine von drei möglichen Normalformen transformieren. Auf diese Weise können Quadriken in verschiedene grundlegende Typen klassifiziert werden. .. weiterlesen
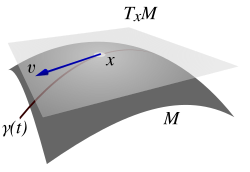
TangentialebeneDie Tangentialebene in einem Punkt an eine Fläche im dreidimensionalen Raum ist diejenige Ebene, die die Fläche in der Umgebung des Punktes am besten annähert (berührt). Sie ist damit die zweidimensionale Entsprechung zur Tangente einer Kurve. Wie im Fall der Kurve existiert eine Tangentialebene nur, wenn die Fläche hinreichend „glatt“ ist. Dies gilt zum Beispiel für die Graphen von differenzierbaren Funktionen von zwei Variablen. Eine Fläche, die einen Knick oder eine Spitze hat – zum Beispiel ein Kegel – besitzt in diesen Punkten keine Tangentialebene. .. weiterlesen