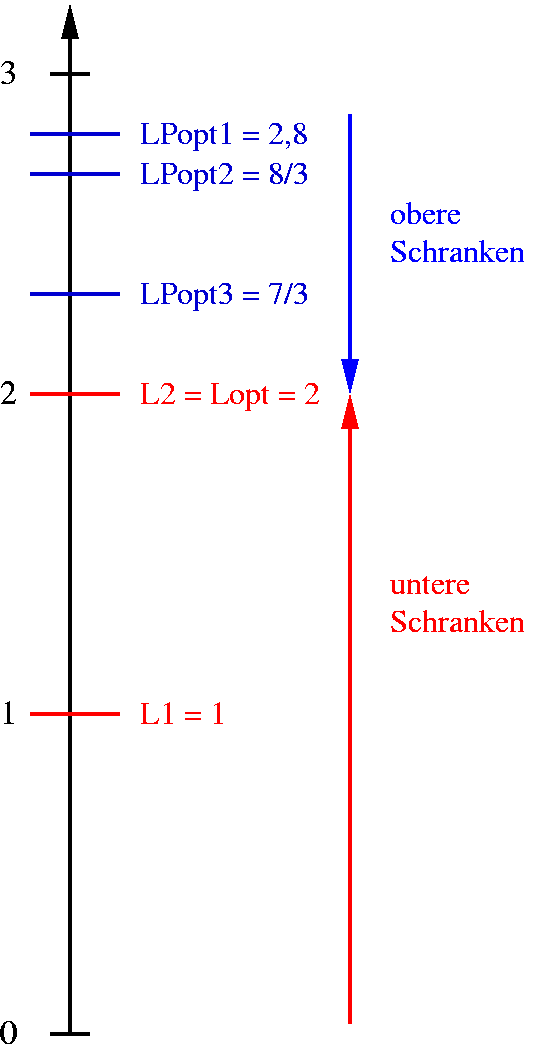
Untere und obere Schranken

Autor/Urheber:

Die Autorenschaft wurde nicht in einer maschinell lesbaren Form angegeben. Es wird Sdo als Autor angenommen (basierend auf den Rechteinhaber-Angaben).

Attribution:

Das Bild ist mit 'Attribution Required' markiert, aber es wurden keine Informationen über die Attribution bereitgestellt. Vermutlich wurde bei Verwendung des MediaWiki-Templates für die CC-BY Lizenzen der Parameter für die Attribution weggelassen. Autoren und Urheber finden für die korrekte Verwendung der Templates hier ein Beispiel.

Shortlink:

https://www.dewiki.de/b/762da

Quelle:

Wikimedia Commons

Größe:

536 x 1044 Pixel (12031 Bytes)

Beschreibung:

Upper and lower bounds in a primal-dual approach for solving an integer program. Self-made using xfig and fig2dev (see http://www.xfig.org/) under Linux. The .fig-files can be obtained from me upon e-mail request.

A .svg version was not displayed correctly, which is why I created a .png file instead.

Lizenz:

CC BY-SA 2.5

Credit:

Die Autorenschaft wurde nicht in einer maschinell lesbaren Form angegeben. Es wird angenommen, dass es sich um ein eigenes Werk handelt (basierend auf den Rechteinhaber-Angaben).

Bild teilen:

         

Weitere Informationen zur Lizenz des Bildes finden Sie hier. Letzte Aktualisierung: Thu, 22 Feb 2024 16:30:05 GMT

Relevante Bilder

Relevante Artikel

Die ganzzahlige lineare Optimierung ist ein Teilgebiet der mathematischen Optimierung. Wie die (kontinuierliche) lineare Optimierung beschäftigt sie sich mit der Optimierung linearer Zielfunktionen über einer Menge, die durch lineare Gleichungen und Ungleichungen eingeschränkt ist. Der Unterschied liegt darin, dass in der ganzzahligen Optimierung alle Variablen nur ganzzahlige Werte annehmen dürfen. Falls nur einige der Entscheidungsvariablen ganzzahlig und andere kontinuierlich sind, so spricht man von einem gemischt-ganzahligen Optimierungsproblem. Im Unterschied zur linearen Optimierung lassen sich mit Hilfe der ganzzahligen linearen Optimierung Optimierungsprobleme modellieren, die aus komplexitätstheoretischer Sicht NP-schwer sind. .. weiterlesen