Line integral of vector field

Autor/Urheber:

Lucas Vieira

Shortlink:

https://dewiki.de/b/14f34c

Quelle:

Wikimedia Commons

Größe:

450 x 410 Pixel (323671 Bytes)

Beschreibung:

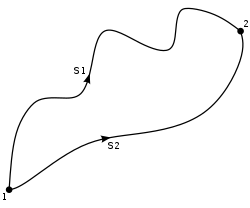
Line integral of a vector field, F.

The particle (in red) travels from point a to point b along a curve C in a vector field F. Shown below, on the dial at right, is the field's vectors from the perspective of the particle. As it changes orientation, the axis arrows rotate to illustrate the changes in reference. The blue arrow is the field vector relative to the current orientation of the particle.

The dot product of the tangent velocity vector (in red) and the field vector (in blue) results in the value represented as a green bar. This bar "sweeps" an area as the particle travels along the path. This area is equivalent to the line integral.

Kommentar zur Lizenz:

Public domainPublic domainfalsefalse

Ich, der Urheberrechtsinhaber dieses Werkes, veröffentliche es als gemeinfrei. Dies gilt weltweit. In manchen Staaten könnte dies rechtlich nicht möglich sein. Sofern dies der Fall ist: Ich gewähre jedem das bedingungslose Recht, dieses Werk für jedweden Zweck zu nutzen, es sei denn, Bedingungen sind gesetzlich erforderlich.

Lizenz:

Public domain

Bild teilen: