Kegelzylinder-mantellinienverf
Relevante Bilder
Relevante Artikel
MantellinienverfahrenDas Mantellinienverfahren ist eine Methode der darstellenden Geometrie, Punkte der Schnittkurve zwischen einem Zylinder und einer zweiten Fläche zu bestimmen. Der wesentliche Teil ist identisch mit dem Hilfsebenenverfahren. Während beim Hilfsebenenverfahren die Hilfsebenen frei gewählt werden, wird beim Mantellinienverfahren von einer gleichmäßig verteilten Anzahl von Mantellinien des Zylinders ausgegangen. Zu jeder Mantellinie wird eine Hilfsebene bestimmt, welche die Mantellinie enthält und aus der zweiten Fläche einfache Kurven ausschneidet. Sind die Mantellinien geschickt gewählt, so enthält eine Hilfsebene gleich zwei Mantellinien, so dass durch eine Hilfsebene gleich mehrere Punkte der Schnittkurve in Grund- und Aufriss konstruiert werden können. Sind die Mantellinien wie im Beispiel gewählt, so haben die Mantellinien 4 und 8 dieselben Grundrisse wie die schon gezeichneten Mantellinien 2 und 10. Für den Schnitt der Hilfsebene durch die Mantellinien 4 und 8 muss also nur der andere Schnittkreis mit dem Kegel in Grund- und Aufriss eingezeichnet werden, um weitere Schnittpunkte zu bestimmen. .. weiterlesen
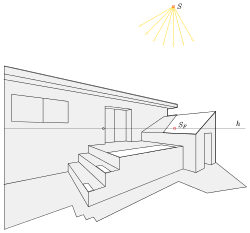
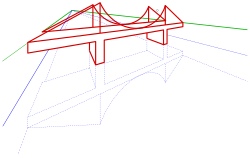
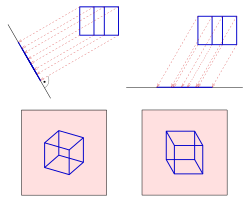
Darstellende GeometrieDarstellende Geometrie ist der Teilbereich der Geometrie, der sich mit den geometrisch-konstruktiven Verfahren von Projektionen dreidimensionaler Objekte auf eine zweidimensionale Darstellungsebene befasst. Die Anwendungsbereiche ihrer Methoden sind breit gefächert und erstrecken sich neben den heute bekanntesten Anwendungen in der Technik- und Architekturdarstellung auch auf Kunst, Malerei, Kartenwesen und Computergraphik. Die Darstellende Geometrie beschränkt sich nicht nur auf das Darstellen von räumlichen Objekten, sondern bietet auch Möglichkeiten raumgeometrische Probleme zeichnerisch zu lösen: z. B. die Bestimmung des Schnittpunktes einer Gerade mit einer Ebene oder die Schnittkurve zweier Flächen oder den Schatten eines Objektes. .. weiterlesen