KUGSPI-9 Loxodrome


Autor/Urheber:
German Wikipedia User Karl Bednarik
Attribution:
Das Bild ist mit 'Attribution Required' markiert, aber es wurden keine Informationen über die Attribution bereitgestellt. Vermutlich wurde bei Verwendung des MediaWiki-Templates für die CC-BY Lizenzen der Parameter für die Attribution weggelassen. Autoren und Urheber finden für die korrekte Verwendung der Templates hier ein Beispiel.
Shortlink:
https://www.dewiki.de/b/35a90
Quelle:
Wikimedia Commons
Größe:
200 x 200 Pixel (60322 Bytes)
Beschreibung:
Ein Loxodrom hat im Gegensatz zur archimedischen Kugelspirale einen konstanten Winkel zwischen den Längengraden und den Breitengraden, der hier das Verhältnis von 10 Länge zu 1 Breite hat.
Kommentar zur Lizenz:
GNU Freie Dokumentationslizenz
Lizenz:
CC BY-SA 3.0
Credit:

GW-BASIC (german wiki)-Programm: 

100 SCREEN 1 : KEY OFF : P=ATN(1)/45 : R=96
110 REM P = WINKEL UMRECHNEN IN RAD : R=RADIUS DER KUGEL
120 REM (REM=REMARK=ANMERKUNG) ZWANZIG BLICKWINKEL ERZEUGEN
130 FOR U = 0 TO 175 STEP 9:T=P*U:G=COS(T):H=SIN(T)
140 CLS : LINE(60,0)-(259,199),3,B : LOCATE 2,9 : PRINT RIGHT$(" "+STR$(U),3);
150 REM BREITENKREISE IN ROT ERZEUGEN
160 FOR V = 90 TO 270 STEP 18 : A=P*V:C=R*COS(A) : Z=R*SIN(A)
170 FOR W = 0 TO 360 STEP (-2*R)/(C-.001) : B=P*W
180 X = C*COS(B) : Y = C*SIN(B) : M = 160 + X : N=100-G*Z-H*Y:O=H*Z-G*Y
190 IF O>-1 THEN PSET(M,N),2
200 NEXT W : NEXT V
210 REM MERIDIANE IN GRUEN ERZEUGEN
220 FOR V = 90 TO 260 STEP 18: A=P*V : E=COS(A) : F=SIN(A)
230 FOR W =  0 TO 360 STEP 2 : B=P*W : Z=R*SIN(B)
240 X = E*R*COS(B) : Y = F*R*COS(B) : M = 160 + X : N = 100 - G*Z - H*Y : O = H*Z - G*Y
250 IF O >- 1 THEN PSET(M,N),1
260 NEXT W : NEXT V : V=90.1 : REM STARTBREITENWINKEL
270 REM LOXODROME IN WEISS ERZEUGEN
280 FOR W = 0 TO 9000 STEP .1
281 B = P*W : V = V + .1*.1*ABS(COS(P*V)) : A = P*V : C = R*COS(A) : Z = R*SIN(A)
290 REM ABS(COS(P*V)) WEIL KLEINER RADIUS = KLEINE STRECKE
300 X = C*COS(B) : Y = C*SIN(B) : M = 160 + X : N = 100 - G*Z - H*Y : O = H*Z - G*Y
310 IF O > -1 THEN PSET(M,N),3
320 NEXT W
330 REM NAECHSTER BLICKWINKEL
340 IF INKEY$="" THEN 340
350 NEXT U : SCREEN 0 : CLS : KEY OFF : WIDTH 80 : LIST : END
360 REM SAVE"KUGSPI-9.BAS",A
Bild teilen:
Facebook   Twitter   Pinterest   WhatsApp   Telegram   E-Mail
Weitere Informationen zur Lizenz des Bildes finden Sie hier. Letzte Aktualisierung: Fri, 14 Mar 2025 15:46:46 GMT

Relevante Bilder


Relevante Artikel

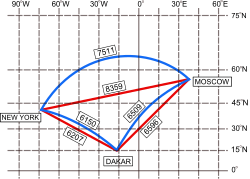
Loxodrome

Eine Loxodrome ist eine Kurve auf einer Kugeloberfläche – z. B. der Erdoberfläche –, die die Meridiane im geographischen Koordinatensystem immer unter dem gleichen Winkel schneidet und daher auch Kursgleiche, Winkelgleiche oder Kurve konstanten Kurses genannt wird. .. weiterlesen

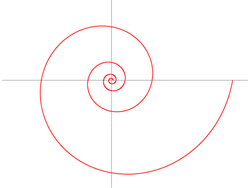
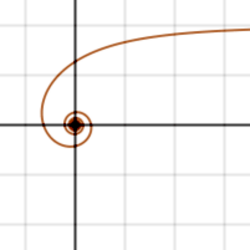
Spirale

Eine Spirale oder Schneckenlinie ist im engeren Sinne eine Kurve, die um einen Punkt oder eine Achse verläuft und sich je nach Betrachterperspektive von diesem Zentrum entfernt oder sich ihm annähert. Im erweiterten Sinne kann es sich dabei statt um einen Punkt, bzw. eine Kurve auch um andere mathematische Objekte wie zum Beispiel Zahlen, Zahlenfolgen oder mathematische Figuren handeln. Zu solchen Spiralen zählen unter anderem die Ulam-Spirale, die Wurzelspirale, die Fibonacci-Spirale oder die aus Dreiecken und Quadraten bestehende Spiralen im Pythagoras-Baum. .. weiterlesen