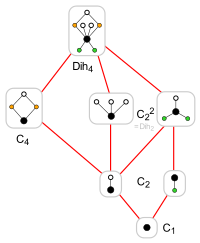
Dih4 subgroups (cycle graphs)

Autor/Urheber:

• Dih4 subgroups.svg: David Eppstein
• derivative work:

Watchduck You can name the author as "T. Piesk", "Tilman Piesk" or "Watchduck".

Shortlink:

https://www.dewiki.de/b/2ffdd5

Quelle:

Wikimedia Commons

Größe:

1009 x 839 Pixel (89287 Bytes)

Beschreibung:

The lattice of subgroups of the dihedral group Dih₄, represented as groups of rotations and reflections of a plane figure.

The subgroups are represented by their cycle graphs.

Kommentar zur Lizenz:

Ich, der Urheber dieses Werkes, veröffentliche es unter der folgenden Lizenz:

Lizenz:

Public domain

Credit:

Dih4 subgroups.svg: 

Bild teilen:

         

Weitere Informationen zur Lizenz des Bildes finden Sie hier. Letzte Aktualisierung: Sat, 27 Jul 2024 08:43:58 GMT

Relevante Artikel

In der Gruppentheorie ist die Frattinigruppe eine spezielle Untergruppe einer gegebenen Gruppe. Mit ihrer Hilfe kann insbesondere die Struktur endlicher p-Gruppen untersucht werden. Sie ist benannt nach dem italienischen Mathematiker Giovanni Frattini, der sie in einem 1885 erschienenen Artikel definiert hat. .. weiterlesen

Eine modulare Gruppe oder M-Gruppe ist eine im mathematischen Teilgebiet der Gruppentheorie betrachtete Art von Gruppen. Es handelt sich um solche Gruppen, deren Verband der Untergruppen ein modularer Verband ist. .. weiterlesen