Zwölfeck

Das Zwölfeck oder Dodekagon (von altgriechisch δωδεκάγωνονdōdekágōnon, deutsch ‚Zwölfeck‘)[1] ist eine geometrische Figur und ein Vieleck (Polygon) mit zwölf Ecken und zwölf Seiten.
Variationen
Das Zwölfeck ist darstellbar als:
- konkaves Zwölfeck, in dem mindestens ein Innenwinkel größer als 180° ist. Ein Zwölfeck kann höchstens sechs solche Winkel haben. Ein konkaves Zwölfeck kann regelmäßig oder unregelmäßig sein.
- konvexes Zwölfeck, in dem alle Innenwinkel kleiner als 180° sind. Ein konvexes Zwölfeck kann regelmäßig oder unregelmäßig sein.
- Sehnenzwölfeck, in dem alle Ecken auf einem gemeinsamen Umkreis liegen, aber die Seitenlängen (Sehnen) möglicherweise ungleich sind.
- regelmäßiges Zwölfeck, es ist bestimmt durch zwölf Punkte auf einem Umkreis. Die benachbarten Punkte haben zueinander stets den gleichen Abstand und sind mittels aneinandergereihten Seiten oder Kanten genannt, verbunden.
- regelmäßiges überschlagenes Zwölfeck, es ergibt sich, wenn beim Verbinden der zwölf Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen , wobei die Anzahl der Eckpunkte angibt und jeder -te Punkt verbunden wird.
- Es gibt nur einen regelmäßigen Zwölfstrahlstern, auch Dodekagramm genannt.
- Die „Sterne“ mit den Symbolen {12/2} und {12/10} sind regelmäßige Sechsecke, {12/3} und {12/9} Quadrate sowie {12/4} und {12/8} gleichseitige Dreiecke.
- Beispiele für gleichseitige und unregelmäßige konkave Zwölfecke
- gleichseitig
- gleichseitig
- unregelmäßig
- unregelmäßig
- Regelmäßiger Zwölfstrahlstern
Regelmäßiges Zwölfeck
Bei einem regelmäßigen Zwölfeck sind alle Seiten gleich lang und alle Eckpunkte liegen auf einem gemeinsamen Umkreis.
Formeln
| Mathematische Formeln zum regelmäßigen Zwölfeck | ||
|---|---|---|
| Flächeninhalt |  | |
| Länge der Diagonalen | ||
| Inkreisradius | ||
| Umkreisradius | ||
| Zentriwinkel | ||
| Innenwinkel | ||
Konstruktion
Ein regelmäßiges Zwölfeck ist mit Zirkel und Lineal konstruierbar.
Bei gegebenem Umkreis
Mit der folgenden Konstruktion erhält man in acht Schritten die zwölf Eckpunkte. Sie gelingt auch mit einem sogenannten kollabierenden Zirkel, da nach dem Ziehen des Umkreises, die vier erforderlichen Kreisbögen stets den gleichen Radius benötigen.
Nach dem Ziehen des Umkreises um seinen Mittelpunkt , wird der erste Eckpunkt des gesuchten Zwölfecks auf dem Umkreis beliebig bestimmt. Es folgt ein Kreisbogen mit dem Radius um ; dabei ergeben sich die nächsten Eckpunkte und sowie der Winkel mit der Winkelweite . Weiterer Kreisbögen mit jeweils dem gleichen Radius werden um die Eckpunkte sowie um die dadurch entstehenden Eckpunkte und gezogen; dabei ergibt sich der Eckpunkt . Mit dem Eintragen der drei Winkelhalbierenden durch bis , durch bis und schließlich durch bis , werden die noch fehlenden Eckpunkte bestimmt. Nach dem Verbinden der nebeneinander liegenden Eckpunkte ist das Zwölfeck fertiggestellt.
Bei gegebener Seitenlänge
Mit der folgenden Konstruktion erhält man in neun Schritten die zweite Seitenlänge . Die Konstruktion ist ähnlich der eines Achtecks bei gegebener Seitenlänge.
Nach dem Festlegen der ersten Seite des gesuchten Zwölfecks, wird um die Eckpunkte und jeweils ein Kreisbogen mit dem Radius gezogen; dabei ergeben sich die Schnittpunkte und . Es folgt eine Halbgerade ab durch und anschließend eine Parallele zu ab bis den Kreisbogen um trifft. Der Winkel wird mittels der Winkelhalbierenden geteilt, dabei bestimmt er den Mittelpunkt des Umkreises. Die anschließende Halbgerade ab durch liefert den Mittelpunktswinkel eines Zwölfecks. Jetzt noch den Umkreis mit Radius ziehen, dabei ergibt sich der Schnittpunkt als dritter Eckpunkt des Zwölfecks. Abschließend werden die noch fehlenden Eckpunkte bestimmt und die nebeneinander liegenden Eckpunkte zu einem Zwölfeck verbunden.
Zerlegung in regelmäßige Polygone
Das regelmäßige Zwölfeck ist außer dem regelmäßigen Sechseck das einzige regelmäßige Polygon, das sich vollständig in regelmäßige Polygone mit einer kleineren Zahl von Ecken zerlegen lässt.
Zerlegungsbeispiele
- 6 gleichseitige Dreiecke,
6 Quadrate und
1 regelmäßiges Sechseck - 12 gleichseitige Dreiecke
und 6 Quadrate - 12 gleichseitige Dreiecke
und 24 gleichschenklige Dreiecke
Flächenbestimmung durch Zerlegung
Mit der Zerlegung in 12 gleichseitige Dreiecke und 24 gleichschenklige Dreiecke lässt sich geometrisch veranschaulichen, dass ein regelmäßiges Zwölfeck mit dem Umkreisradius 1 die Flächenmaßzahl 3 hat.[2][3]
Eine solche Zerlegung hat folgende Eigenschaften:
- 12 kongruente gleichseitige (braune) Dreiecke mit der Seitenlänge des Zwölfecks,
- 24 kongruente gleichschenklige (gelbe) Dreiecke, deren Grundseitenlänge 1 gleich dem Umkreisradius und deren Schenkellänge gleich der Seitenlänge des Zwölfecks ist (Figur 1).
Das dem Zwölfeck umbeschriebene Quadrat hat die Flächenmaßzahl 4 (Figur 2).
Werden dem Zwölfeck 3 der 12 gleichseitigen Dreiecke (dunkelgrau) und 6 der 24 gleichschenkligen Dreiecke (hellgrau) entnommen, so lassen sich diese lückenlos zwischen dem Zwölfeck und dem umbeschriebenen Quadrat platzieren (Figur 3).
Somit hat das Zwölfeck die Flächenmaßzahl 3 (gesamte gefärbte Fläche).
- Figur 1
- Figur 2
- Figur 3
Quadratur eines regelmäßigen Zwölfecks
Durch geeignete jeweilige Zerlegung in Teilflächen lässt sich sowohl ein konvexes als auch ein konkaves regelmäßiges Zwölfeck in ein flächengleiches Quadrat verwandeln.[4][5]
- Verwandlung eines konvexen regelmäßigen Zwölfecks in ein flächengleiches Quadrat
- Verwandlung eines konkaven regelmäßigen Zwölfecks in ein flächengleiches Quadrat
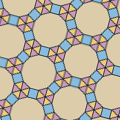
Parkettierungen mit regelmäßigen Zwölfecken
Mit regelmäßigen Zwölfecken sind eine Vielzahl von Parkettierungen möglich. Die ersten zwei sind archimedische Parkettierungen, die dritte eine demireguläre Parkettierung:
- 3-12-12
- 4-6-12
- 3-3-4-12 und 3-3-3-3-3-3
Die Zahlen unter den Abbildungen geben an, wie viele Ecken die regelmäßigen Polygone haben, die jeweils an einem Punkt zusammenstoßen. Die Innenwinkel ergeben zusammen 360°. Diese Parkettierungen sind periodisch, drehsymmetrisch und translationssymmetrisch und enthält ausschließlich regelmäßige Polygone.
Ein Beispiel für eine kommerziell genutzte Parkettierung ist das Eternity-Puzzle, ein Legespiel, bei dem 209 unregelmäßige Polygonspielsteine zu einem Zwölfeck gelegt werden sollen.
Zwölfeck in der Numismatik
Es gibt eine Vielzahl zwölfeckiger Münzen, z. B. das britische Threepence von 1942, die ehemalige 3–Pence–Münze aus Nigeria und die australische 50-cent-Münze, die 50-¢(= Seniti)-Münze von Tonga, sowie spezielle Sammlermünzen wie z. B. die spanische 300–Euro–Münze.

Zwölfeck in der Architektur
Deutschland

- das Panorama Kreuzigung Christi (Altötting)
- die Neue Synagoge Berlin – Centrum Judaicum (Berlin)
- das Zwölfeckhaus in Ottendorf-Okrilla bei Dresden
- das Mausoleum des Hauses Pfalz-Neuburg in Düsseldorf
- die St.-Petrus-Kirche in Gesmold
- Apostelkirche (Greding)
- das Schloss Großsachsenheim
- viele der Hamburger Fahrradhäuschen
- das Planetarium Leipzig
- der Dianatempel (ein zwölfeckiger Pavillon) in München
- Zwölf-Apostel-Kirche (Mannheim)
- Zwölfeck-Faltdachkuppelpyramide der Kirche Verklärung Christi (Neustadt bei Coburg)
- Reformations-Gedächtnis-Kirche (Nürnberg)
- der Wasserturm Plattling
- der Wasserturm Schifferstadt
- Wasserturm im Kurpark (Wilhelmshaven), Oberteil über runder Basis
- Wasserkunst Wismar
- die Gertrudenkapelle in Wolgast (Mecklenburg-Vorpommern)
Weitere

Beispiele für Gebäude mit Zwölfeckstruktur sind:
- die Reformierte Kirche in Budapest, Ungarn
- die Vera-Cruz-Kirche in Segovia, Spanien
- der Pavillon des Letná-Karussells in Prag, Tschechien
- der gläserne Kiosk der Tankstelle Auto Palace, Niederlande
- die Pagode des Songyue-Tempels der Stadt Dengfeng, China
- das Chorhaupt von St-Pierre-et-St-Paul de Maguelone, Grundriss aus halbiertem Zwölfeck
- Musikpavillon Baden bei Wien, halbiertes Zwölfeck
- die Jeruzalemkapel in Gouda, Provinz Südholland, Niederlande
- die kanadische Kirche St. Vincent de Paul Church (Niagara-on-the-Lake) mit einem 1965 vorgesetztem Zwölfeckanbau
Zwölfeck in der Chemie


Das Molekülmodell von Cyclododecan ist nur in der Draufsicht zwölfeckig. Aus der dreidimensionalen Gestalt dieses Moleküls ergibt sich, dass die Kohlenstoffatome nicht alle in einer Ebene liegen. Außerdem befindet sich das Molekül bei höherer Temperatur in ständiger Bewegung, nämlich in Pseudorotation, d. h., es existieren eine Vielzahl von Konformationen.
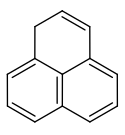
Ein gleichseitiges konkaves Zwölfeck wird vom Phenalen, einem polycyclischen aromatischen Kohlenwasserstoff, gebildet.
Weblinks
- Eric W. Weisstein: Dodecagon. In: MathWorld (englisch).
Einzelnachweise
- ↑ Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914 (zeno.org [abgerufen am 2. Juli 2024]).
- ↑ Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 161
- ↑ Ross Honsberger: Mathematical Gems III, Mathematical Association of America, Washington 1985, S. 31
- ↑ Martin Gardner: Mathematische Knobeleien, Friedr. Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig 1984, ISBN 978-3-528-28321-6, Seite 44
- ↑ Harry Lindgren: Geometric Dissections - Mathematics for everyday living series, Verlag Van Nostrand, 1964
Auf dieser Seite verwendete Medien
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Zwölfeck bei gegebenem Umkreis
Autor/Urheber: Mabit1, Lizenz: CC BY-SA 4.0
Zerlegung eines regelmäßigen Zwölfecks
Autor/Urheber: Luidger, Lizenz: CC BY-SA 3.0
Templerkirche Vera Cruz (Segovia, Spanien)
Autor/Urheber: Mabit1, Lizenz: CC BY-SA 4.0
Zerlegung eines regelmäßigen Zwölfecks
Autor/Urheber: Allie_Caulfield from Germany, Lizenz: CC BY 2.0
Altötting, Panorama Kreuzigung Christi, Außenansicht des Gebäudes
This coin is listed in the Standard Catalogue of British Coins under the ID 4112.
Autor/Urheber: R. A. Nonenmacher, Lizenz: CC BY-SA 4.0
Semiregular Tiling 3-12-12 (Truncated Hexagonal)
Autor/Urheber: Mabit1, Lizenz: CC BY-SA 4.0
Verwandlung eines konvexen regelmäßigen Zwölfecks in ein flächengleiches Quadrat durch Zerlegung in Teilflächen
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Zwölfstrahlstern mit Schläfli-Symbolen 12/5, 12/7
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Zwölfeck bei gegebener Seitenlänge
Autor/Urheber: Mabit1, Lizenz: CC BY-SA 4.0
Verwandlung eines konkaven regelmäßigen Zwölfecks in ein flächengleiches Quadrat durch Zerlegung in Teilflächen
Autor/Urheber: Baelde, Lizenz: CC BY-SA 3.0
The image evokes a covering of the entire Euclidean plane with an infinity of convex regular polygons: equilateral triangles, squares, dodecagons. All polygons with the same number of sides are congruent. Every side of any polygon is shared by two polygons: they are placed side to side.
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Zwölfeck bei gegebener Seitenlänge, Animation
Autor/Urheber: Jynto (talk), Lizenz: CC0
Ball-and-stick model of the cyclododecane molecule, a cycloalkane with 12 carbon atoms.
Colour code:
- Carbon, C: black
- Hydrogen, H: white
Autor/Urheber: User:Tomruen and User:KSFT, Lizenz: CC BY-SA 4.0
Dodecagon, divided into triangles and squares
Struktur des Phenalens
Autor/Urheber: KSFT, Lizenz: CC BY-SA 4.0
This is an SVG version of File:Hexagonal cupola flat.png.
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Zwölfeck mit eingetragenen Gößen
Autor/Urheber: R. A. Nonenmacher, Lizenz: CC BY-SA 4.0
Semiregular Tiling 4-6-12 (Great Rhombitrihexagonal)
Autor/Urheber: László Németh, Lizenz: CC0
Regular dodecagon with annotation.
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Zwölfeck bei gegebenem Umkreis, Animation, 15 s Pause
Autor/Urheber: Mabit1, Lizenz: CC BY-SA 4.0
Zerlegung eines regelmäßigen Zwölfecks