Trigonometrische Funktion

Mit trigonometrischen Funktionen auch Winkelfunktionen (seltener: Kreisfunktionen oder goniometrische Funktionen) bezeichnet man rechnerische Zusammenhänge zwischen Winkel und Seitenverhältnissen (ursprünglich in rechtwinkligen Dreiecken). Tabellen mit Verhältniswerten für bestimmte Winkel ermöglichen Berechnungen bei Vermessungsaufgaben, die Winkel und Seitenlängen in Dreiecken nutzen. Die trigonometrischen Funktionen sind außerdem die grundlegenden Funktionen zur Beschreibung periodischer Vorgänge in den Naturwissenschaften.


Die elementaren trigonometrischen Funktionen sind:
- die Sinusfunktion (abgekürzt: sin)
- die Kosinusfunktion (abgekürzt: cos)
- die Tangensfunktion (abgekürzt: tan oder tg)
sowie deren Kehrwerte:
- Kosekansfunktion (Kehrwert des Sinus: csc)
- Sekansfunktion (Kehrwert des Kosinus: sec)
- Kotangensfunktion (Kehrwert des Tangens: cot)
Zwischen diesen Funktionen bestehen enge Zusammenhänge. Genau genommen würde bereits eine der Funktionen ausreichen, um beliebige trigonometrische Probleme lösen zu können. Die Verwendung mehrerer verschiedener Funktionen ermöglicht jedoch eine Vereinfachung der Rechnungen und Formeln.
Die Kotangensfunktion wird in Tabellen mit Funktionswerten von trigonometrischen Funktionen gerne genutzt, da man cot(x) zusammen mit der Tangensfunktion tabellieren kann. Insofern ist die Bedeutung von cot(x) etwas größer als die von sec(x) und csc(x).
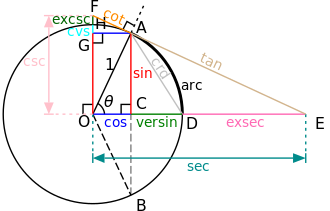
Es gibt weitere – heute eher unübliche – Funktionen, wie z. B. sinus versus (versin), cosinus versus (coversin), exsecant (exsec) und excosecant (excsc).
Definition
Trigonometrisch in der Elementargeometrie
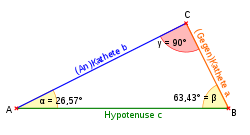
Ursprünglich (und im überwiegenden Schulgebrauch) sind die Winkelfunktionen in der Euklidischen Geometrie als Seitenverhältnisse in rechtwinkligen Dreiecken und daher nur für Winkel von 0 bis 90 Grad definiert:
Diese Definition ist unabhängig von der Wahl des rechtwinkligen Dreiecks, das zur Berechnung verwendet wird. In jedem rechtwinkligen Dreieck mit gleichem Winkel ergeben diese Verhältnisse den gleichen Wert. Dies lässt sich z. B. mit den Strahlensätzen beweisen.
Aus diesen Beziehungen folgt unmittelbar die Beziehung:
Die Ankathete des Winkels ist gleichzeitig die Gegenkathete des anderen spitzen Winkels des rechtwinkligen Dreiecks; da die Winkelsumme im Dreieck 180° beträgt, und der rechte Winkel 90° zu dieser Summe beiträgt, ist dieser Winkel und daher
Geometrisch am Einheitskreis
Die Winkelfunktionen können aber als Sekanten- und Tangentenabschnitte am Einheitskreis auch auf größere Winkel erweitert werden. Vom Schnittpunkt des einen Winkelschenkels mit dem Einheitskreis werden die Lote auf die beiden Koordinatenachsen gefällt und liefern Sinus und Kosinus des Winkels. Die Tangenten in den Punkten x = 1 bzw. y = 1 schneiden den Schenkel ebenfalls und liefern dann in der Projektion auf die Achsen den Tangens und den Kotangens. Dabei muss der Schenkel gegebenenfalls rückwärts verlängert werden, um einen Schnittpunkt zu erzielen. Auf diese Weise können jedem Winkel von 0 bis 360 Grad Werte der Winkelfunktionen zugeordnet werden, die nun freilich auch negativ werden können (siehe Abbildung). Die oben angegebenen Beziehungen gelten dabei weiterhin.
In der Analysis
In der Höheren Mathematik (zB. in der Analysis) werden Sinus und Kosinus in der Regel vollständig für beliebige reelle oder komplexe Zahlen über Potenzreihen definiert, wobei der Winkel im Bogenmaß angegeben wird. Ein Geometriebezug ist dabei nicht notwendig. In der Komplexen Analysis (Funktionentheorie) wird zum Beispiel zuerst die Exponentialfunktion als Reihe definiert und dann Sinus und Kosinus über die gliedweise Differenz und Summe der Reihen als und . Für reelle Argumente erhält man die Eulersche Formel mit Zerlegung in Real- und Imaginärteil als . Die komplexen Sinus- und Kosinusfunktionen sind in der gesamten komplexen Zahlenebene analytisch und somit ganze Funktionen. Die komplexen Tangens-, Kotangens, Sekans- und Kosekansfunktionen sind in der gesamten komplexen Zahlenebene meromorph. Alle sechs trigonometrischen Funktionen sind in der komplexen Zahlenebene einfach periodisch.
Näheres siehe in den Artikeln Sinus und Kosinus, Tangens und Kotangens, Exponentialfunktion und Eulersche Formel.
Beziehungen zwischen den Funktionen
Die Vorzeichen der trigonometrischen Funktionen in Abhängigkeit vom Quadranten gibt die folgende Tabelle an:
| Quadrant | sin und csc | cos und sec | tan und cot |
|---|---|---|---|
| I | + | + | + |
| II | + | − | − |
| III | − | − | + |
| IV | − | + | − |
Der Betrag wird wie folgt umgerechnet:
| sin | cos | tan | cot | sec | csc | |
|---|---|---|---|---|---|---|
| sin(x) | ||||||
| cos(x) | ||||||
| tan(x) | ||||||
| cot(x) | ||||||
| sec(x) | ||||||
| csc(x) |
Wenn das verwendet wird, ist zu beachten, dass
- für oder
- für oder
- für oder
- für oder
- für oder
- für oder
- für oder
- für oder
- für oder
- für oder
- für oder
- für oder
Ungleichungen zwischen den Funktionen

In den nachfolgenden Ungleichungen, die auf den griechischen Astronomen und Mathematiker Aristarchos von Samos zurückgehen, werden Verhältnisse zwischen den Argumenten und den Funktionswerten trigonometrischer Funktionen miteinander verglichen. Sie lautet:
Aus der abgebildeten Figur resultieren der Beweisansätze
und
- .
Dividiert man die erste dieser beiden letzten Ungleichungen durch und die zweite durch , so erhält man durch Zusammenführung der so umgeformten Ungleichungen
- ,
Anwendung
Unter anderem werden die trigonometrischen Funktionen im Vermessungswesen genutzt. Formeln zur Berechnung von Größen am Dreieck → Dreiecksgeometrie.
Weiterhin sind sie in der Analysis und bei vielen Anwendungen der Physik und der Technik wichtig. Es besteht eine enge Beziehung zur Exponentialfunktion, die besonders bei Funktionen komplexer Zahlen und in der Taylorreihe der Funktionen sichtbar wird.
Umkehrung
In manchen Situationen werden die trigonometrischen Winkelfunktionen benötigt, um aus Seitenverhältnissen Winkel zu berechnen. Dazu werden die Arkusfunktionen oder inverse Winkelfunktionen arcsin, arccos, arctan und arccot – die Umkehrfunktionen zu den trigonometrischen Funktionen – verwendet. Auf Taschenrechnern sind sie häufig mit sin−1 usw. bezeichnet. Das stimmt mit der Schreibweise für die Umkehrfunktion von f überein (auch wenn die Arkusfunktionen das genau genommen nicht sind), kollidiert allerdings mit der ebenso üblichen Konvention, für zu schreiben.
Die Arkusfunktionen werden verwendet, um zu einem Seitenverhältnis den Winkel zu berechnen. Wegen der Symmetrie der trigonometrischen Funktionen ist von Fall zu Fall zu klären, in welchem Quadrant der gesuchte Winkel liegt.
Siehe auch
Weblinks
- Interaktive Darstellung der trigonometrischen Funktionen am Einheitskreis. In: GeoGebra.
- Inverse Winkelfunktionen
Einzelnachweise
- ↑ Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 146
- ↑ Mathematics Magazine, vol. 66, no. 1 (Feb. 1993), S. 65
Auf dieser Seite verwendete Medien
Autor/Urheber: MartinThoma, Lizenz: CC0
Die Trigonometrischen Funktionen am Einheitskreis:
Die Winkelfunktionen im Einheitskreis.
Autor/Urheber: PaterSigmund (Original by Cweiske), Lizenz: CC BY-SA 2.5
Rechtwinkliges Dreieck
Autor/Urheber: Mabit1, Lizenz: CC BY-SA 4.0
Grafische Veranschaulichung der Ungleichung von Aristarchos
We have the unit circle (with radius = 1) in green, placed at the origin at the bottom right.
In the middle of this circle, in yellow, is represented the angle theta (θ). This angle is the amount of counter-clockwise rotation around the circle starting from the right, on the x-axis, as illustrated. An exact copy of this little angle is shown at the top right, as a visual illustration of the definition of θ.
At this angle, and starting at the origin, a (faint) green line is traced outwards, radially. This line intersects the unit circle at a single point, which is the green point spinning around at a constant rate as the angle θ changes, also at a constant rate.
The vertical position of this point is projected straight (along the faint red line) onto the graph on the left of the circle. This results in the red point. The y-coordinate of this red point (the same as the y-coordinate of the green point) is the value of the sine function evaluated at the angle θ, that is:
- y coordinate of green point = sin θ
As the angle θ changes, the red point moves up and down, tracing the red graph. This is the graph for the sine function. The faint vertical lines seen passing to the left are marking every quadrant along the circle, that is, at every angle of 90° or π/2 radians. Notice how the sine curve goes from 1, to zero, to -1, then back to zero, at exactly these lines. This is reflecting the fact sin(0) = 0, sin(π/2) =1, sin(π) = 0 and sin(3π/ 2) -1
A similar process is done with the x-coordinate of the green point. However, since the x-coordinate is tilted from the usual convention to plot graphs (where y = f(x), with y vertical and x horizontal), an “untilt” operation was performed in order to repeat the process again in the same orientation, instead of vertically. This was represented by a “bend”, seen on the top right.
Again, the green point is projected upwards (along the faint blue line) and this “bent” projection ends up in the top graph’s rightmost edge, at the blue point. The y-coordinate of this blue point (which, due to the “bend” in the projection, is the same as the x-coordinate of the green point) is the value of the cosine function evaluated at the angle θ, that is:
- x coordinate of green point = cos θ
Autor/Urheber: Geek3, Lizenz: CC BY 3.0
Plot of all six trigonometric functions in the interval [-2π,2π]:
- y1(x) = arcsin(x)
- y2(x) = arccos(x)
- y3(x) = arctan(x)
- y4(x) = arccot(x)
- y5(x) = arcsec(x)
- y6(x) = arccsc(x)
Autor/Urheber:
This is a graphical construction of the various trigonometric functions from a chord AD (angle θ) of the unit circle centered at O. In addition to the modern trigonometric functions sin (sine), cos (cosine), tan (tangent), cot (cotangent), sec (secant), and csc (cosecant), the diagram also includes a few trigonometric functions that have fallen into disuse: chord, versin (versine or versed sine), exsec (exsecant), cvs (coversine), and excsc (excosecant).