Symmetriegruppe
In der mathematischen Gruppentheorie ist die Symmetriegruppe eines geometrischen Objektes die Gruppe, die aus der Menge aller Kongruenzabbildungen besteht, die das Objekt auf sich selbst abbilden, zusammen mit der Verkettung von Abbildungen als Gruppenverknüpfung.
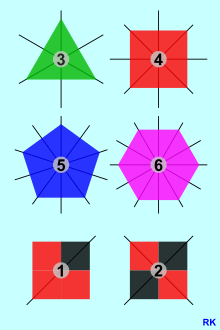
Die Grafik zeigt sechs zweidimensionale symmetrische Objekte, und zwar vier homogene reguläre Polygone und zwei weitere geometrische Figuren, wobei jeweils alle ihre Symmetrieelemente gekennzeichnet worden sind. Die Symmetrieelemente sind Eigenschaften der Figuren. Die Gesamtheit der Symmetrieelemente einer Figur bildet ihre spezielle Symmetriegruppe.
Rotationssymmetrie und Spiegelsymmetrie an Beispielen
Untersucht man eine geometrische Figur auf ihre Symmetrien, so kommt man zunächst ganz ohne den mathematischen Begriff Gruppe aus. Es ist vielleicht günstig, wenn sich Einsteiger in das Gebiet Symmetriegruppen an die Herangehensweise des Mathematikers, Physikers und Philosophen Hermann Weyl halten. Weyl, einer der Pioniere der Gruppentheorie, beginnt das Vorwort seines berühmten Buchs Symmetrie[1] so:
- Beginnend mit der etwas vagen Vorstellung von Symmetrie als Harmonie der Proportionen entwickeln diese vier Vorträge stufenweise zuerst den Begriff der geometrischen Symmetrie in ihren verschiedenen Formen als bilaterale,[2] translative, rotative, ornamentale und kristallographische Symmetrie und steigen schließlich zu der allgemeinen, all diesen Formen zugrunde liegenden Idee auf, nämlich der Idee der Invarianz eines Gebildes gegenüber einer Gruppe automorpher Transformationen.
Eine Figur ist rotationssymmetrisch, wenn sie von der Figur nicht zu unterscheiden ist, die sich ergibt, wenn sie um einen zentralen Punkt um den Winkel gedreht wird. Ein Kreis oder ein Kreisring sind rotationssymmetrisch im engeren Sinne. Eine Drehung um jeden beliebigen Winkel bildet sie auf sich selbst ab.
Rotationssymmetrisch (oder auch drehsymmetrisch[3]) wird eine Figur auch dann genannt, wenn sie auf sich abgebildet werden kann, indem sie um einen festen Winkel mit 0°<< 360° um den zentralen Punkt gedreht wird. Der Drehwinkel kann nur durch Division des vollen Winkels durch eine natürliche Zahl >1 entstehen, also . Diese Zahl ist eine Kennzahl der Rotationssymmetrie und wird auch „Zähligkeit“ genannt.[4] Entsprechend heißt diese Symmetrie auch -zählige oder -fache Rotationssymmetrie/Drehsymmetrie, im Englischen „-fold rotational symmetry“. Dabei wird die neutrale Symmetrieoperation stets mitgezählt. Damit bezeichnet man „keine Operation“, also die „Operation“, die die Figur in ihrer Ausgangsstellung belässt. Sie unterscheidet sich nicht von der einer Drehung der Figur um .
Reguläre Polygone sind typische rotationssymmetrische Figuren. Die Grafik zeigt die ersten vier, wobei die jeweils größtmögliche Kennzahl der Rotationssymmetrie zentral eingezeichnet worden ist. Außerdem sind zwei weitere Figuren dargestellt, und zwar eine ohne und eine mit 2-facher Rotationssymmetrie. Im Trivialfall liegt keine Rotationssymmetrie/Drehsymmetrie vor und die Kennzahl 1 wird im mathematischen Kontext nicht verwendet, es sei denn, man möchte die triviale zyklische Gruppe kennzeichnen, die nur aus der identischen Abbildung besteht.
Eine Figur ist dann spiegelsymmetrisch, wenn sie an einer der Spiegelsymmetrieachsen gespiegelt wird und wenn sie von ihrem Abbild, das so entsteht, nicht zu unterscheiden ist. Alle abgebildeten Figuren sind spiegelsymmetrisch. Sie besitzen 3, 4, 5, 6, 1 bzw. 2 Spiegelsymmetrieachsen. Homogene reguläre Polygone besitzen so viele Spiegelsymmetrieachsen, wie sie Rotationssymmetrieelemente besitzen (wenn man die neutrale Symmetrieoperation zu den Rotationssymmetrieelementen zählt). Der Umkehrschluss gilt nicht: Eine Figur mit n-facher Rotationssymmetrie braucht nicht unbedingt Spiegelsymmetrieachsen zu besitzen. Auch gilt: Besitzt eine Figur eine Spiegelsymmetrieachse, muss sie nicht unbedingt auch rotationssymmetrisch sein, wie die Figur in der linken unteren Ecke der Grafik zeigt.
Zur Symmetriegruppe der jeweiligen Figur kommt man, indem man die Symmetrien der jeweiligen Figur, des jeweiligen Objekts systematisiert.
Begriffsklärung
Die nachfolgenden Begriffe beschreiben mögliche Eigenschaften eines Objekts, anhand derer festgestellt werden kann, welcher Symmetriegruppe das Objekt angehört.
Diskretheit
Eine Symmetriegruppe weist dann eine diskrete Topologie auf, wenn es so etwas wie „kleinste Schritte“ gibt. Beispielsweise ist eine Gruppe von Drehungen um einen Punkt genau dann diskret, wenn alle möglichen Drehwinkel Vielfache eines kleinsten Winkels sind. Sind hingegen auch beliebig kleine Drehwinkel in der Gruppe enthalten, so ist diese Gruppe nicht diskret. Allgemein hat jede Gruppe mit endlich vielen Elementen eine diskrete Topologie. Eine diskrete Gruppe lässt sich aus endlich vielen Symmetrieoperationen durch Komposition erzeugen. Der Umkehrschluss gilt jeweils nicht.
Praktisch gesehen ist eine Symmetriegruppe genau dann diskret, wenn es eine untere Schranke gibt, sowohl für die Längen aller (von Null verschiedenen) Verschiebungen als auch für die Drehwinkel aller Drehsymmetrien.
Periodizität
Man betrachtet die Menge aller in der Gruppe enthaltenen (von Null verschiedenen) Verschiebungen (Translationen) und bestimmt, wie viele dieser Vektoren linear unabhängig voneinander sind, man bestimmt also die Dimension der linearen Hülle dieser Verschiebungsvektoren.
Enthält die Gruppe überhaupt keine Verschiebungen, so gibt es mindestens einen Punkt, der Fixpunkt aller Abbildungen ist. Man spricht in diesem Fall von einer Punktgruppe. Punktgruppen sind genau dann endlich, wenn sie diskret sind.
Sobald die Gruppe mindestens eine Verschiebung enthält, enthält sie zumindest in euklidischer Geometrie automatisch unendlich viele Elemente.
Entspricht die Zahl der linear unabhängigen Verschiebungsvektoren der Dimension des Raumes, in den das Objekt eingebettet ist, so gibt es einen beschränkten Teil des Objekts (eine Zelle), deren Bilder den gesamten Raum ausfüllen. Ist die Gruppe zusätzlich auch noch diskret, so spricht man von einer Raumgruppe und nennt das Muster periodisch. In diesem Fall gibt es einen beschränkten Fundamentalbereich von gleicher Dimension wie der Raum, also beispielsweise in der Ebene eine entsprechende von Null verschiedene Fläche.
Zweidimensionale euklidische Geometrie
Die Symmetriegruppen in der euklidischen Ebene lassen sich wie folgt klassifizieren:
- Diskret
- Ohne Verschiebungen
- Ohne Achsenspiegelungen
- Familie der endlichen zyklischen Gruppen (für ), das sind alle Drehungen um einen Punkt um Vielfache von
- : Symmetriegruppe eines komplett unsymmetrischen Objektes, mit der Identität als einzigem Element
- : Symmetriegruppe einer Punktspiegelung
- : Symmetriegruppe einer Triskele
- : Symmetriegruppe einer Swastika
- : Symmetriegruppe einer Punktspiegelung
- : Symmetriegruppe eines komplett unsymmetrischen Objektes, mit der Identität als einzigem Element
- Familie der endlichen zyklischen Gruppen (für ), das sind alle Drehungen um einen Punkt um Vielfache von
- Mit Achsenspiegelungen
- Familie der Diedergruppen (für ), das sind Drehungen wie zusammen mit Spiegelachsen durch den Mittelpunkt
- : Einzelne Achsenspiegelung
- : Symmetriegruppe eines nicht quadratischen Rechtecks, einer nicht quadratischen Raute (D2 ist isomorph zur Kleinschen Vierergruppe)
- : Symmetriegruppe eines regelmäßigen n-Ecks
- : Symmetriegruppe eines nicht quadratischen Rechtecks, einer nicht quadratischen Raute (D2 ist isomorph zur Kleinschen Vierergruppe)
- : Einzelne Achsenspiegelung
- Familie der Diedergruppen (für ), das sind Drehungen wie zusammen mit Spiegelachsen durch den Mittelpunkt
- Ohne Achsenspiegelungen
- Mit Verschiebungen, die alle kollinear sind (Span der Translationen hat Rang 1)
- 7 Friesgruppen
- Mit mindestens zwei linear unabhängigen Verschiebungen
- Ohne Verschiebungen
- Nicht diskret
- Ohne Verschiebungen
- Orthogonale Gruppe , das sind alle Symmetrien eines Kreises, also alle Drehungen und alle Spiegelungen an Achsen, die durch den Mittelpunkt gehen
- Mit Verschiebungen
- Dieser Fall muss noch weiter aufgeschlüsselt werden.
- Ohne Verschiebungen
Andere Dimensionen
- Dreidimensionale Punktgruppen werden in einem eigenen Artikel ausführlich klassifiziert.
- Der Artikel über Raumgruppen geht auch auf verschiedene Dimensionen ein.
Literatur
- Willard Miller, Jr.: Symmetry Groups and Their Applications. Academic Press, New York, London 1972, ISBN 0-12-497460-0 (x, 432, archive.org – In diesem einführenden Lehrbuch werden diejenigen Aspekte der Gruppentheorie behandelt, die in den Naturwissenschaften nützlich sind, ohne dass dabei auf mathematische Strenge verzichtet wird).
- M. S. Dresselhaus: Group Theory – Application to the Physics of Condensated Matter. Springer Verlag, Heidelberg 2008, ISBN 978-3-540-32897-1.
- Michael Tinkham: Group Theory and Quantum Mechanics. Dover Pubn Inc – 1. Januar 2004, ISBN 0-486-43247-5.
Einzelnachweise
- ↑ Hermann Weyl: Symmetrie: Ergänzt durch den Text „Symmetry and Congruence'“ aus dem Nachlass und mit Kommentaren von Domenico Giulini, Erhard Scholz und Klaus Volkert. Übersetzerin Lulu Hofmann Bechtolsheim. 3. Auflage. Springer Spektrum, Berlin, Heidelberg 2017, ISBN 978-3-662-52711-5 (VII, 232, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 23. Juli 2019]). Reprint des Originals von 1952 in Hermann Weyl: Symmetry. Princeton University Press, Princeton, NJ 2015 (176 S., eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 23. Juli 2019]).
- ↑ Weyl nennt die Spiegelsymmetrie auch bilaterale Symmetrie (s. Bilateralität), also eine zweiseitige Symmetrie, weil eine Spiegelsymmetrieebene eine Figur in zwei gleiche oder ein Tier in zwei äußerlich gleich aussehende spiegelbildliche Hälften teilt. Im Tierreich ist Bilateralität die typische Symmetrieform des Körpers. Rund 95 Prozent der vielzelligen Tierarten gehören zu den Bilateria, den „Zweiseitentieren“.
- ↑ Drehsymmetrie. Abgerufen am 26. April 2023.
- ↑ Symmetrie. Abgerufen am 20. Juni 2019.
Siehe auch
- Symmetrie (Geometrie)
- Symmetrische Gruppe aller Permutationen mit Elementen
- Kristallographie
- Symmetrie (Physik)
Weblinks
Auf dieser Seite verwendete Medien
Autor/Urheber: Roderich Kahn, Lizenz: CC BY-SA 4.0
Vier reguläre Polygone und zwei weitere geometrische Figuren mit den Kennzahlen ihrer Rotationssymmetrien und ihren Spiegelsymmetriegeraden
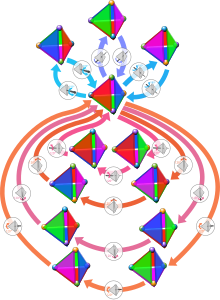
(c) Debivort, CC BY-SA 3.0

tetrahedral symmetry group. created by me user debivort august 2006.
SVG format may have bugs fixed relative to previous version.