Normwert

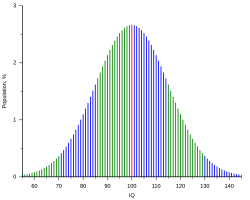
Normwert ist ein Begriff aus der Psychologie und aus der Medizin. Der Normwert dient dazu, die Eigenschaften eines Individuums in Bezug zur Gesamtheit aller Individuen einzuordnen. Normwerte werden gewonnen, indem ein Forscher mit einer Messmethode eine ausreichend große Stichprobe der zu untersuchenden Grundgesamtheit untersucht und dadurch eine individuelle Eigenschaftsausprägung einordbar wird. In der Regel wird hierbei eine quasi kontinuierliche Verteilung der Ausprägung einer Eigenschaftsqualität unterstellt. Der ursprüngliche Messwert wird Rohwert genannt.

Nach Erstellung der Normwerte kann ein anderer Forscher oder Untersucher eine Person mit der gleichen Messmethode untersuchen und das Individuum dann in Beziehung zur Grundgesamtheit der Normstichprobe setzen. Weiterhin lässt sich die Ausprägung verschiedener Eigenschaften einer Person beurteilen, indem diese über die Normwerte vergleichbar werden. Die Normstichprobe sollte so groß sein, dass sie ein repräsentatives Abbild der Grundgesamtheit darstellen kann. Ebenfalls ist es sinnvoll, die Normstichprobe anhand bestimmter Merkmale zu kategorisieren und den Normwert entsprechend den Merkmalen zu bestimmen. Zum Beispiel kann die Normstichprobe für einen Intelligenztest in verschiedene Altersgruppen und nach Geschlecht unterteilt sein. Zusätzlich könnte eine weitere Einteilung anhand des Bildungsstandes erfolgen.

Normwertskalen

Es existieren verschiedene Normwertskalen, die direkt ineinander umgerechnet werden können. Die bekannteste dieser Skalen ist die IQ-Skala. Ein IQ-Wert von 100 entspricht exakt dem Mittelwert. Weitere Skalen sind die z-Skala, die T-Wert-Skala, der Stanine-Wert, die Centil- (C-Skala) und die Standardwert-Skala (SW-Skala). Von diesen Skalen unterscheidet sich der Prozentrang (PR), der angibt, welcher Prozentsatz der Normstichprobe eine gleich hohe oder kleinere Eigenschaftsausprägung aufweist. Ein PR von 50 bedeutet ein durchschnittliches Ergebnis, ein PR von 10 dagegen, dass nur 10 % der Normstichprobe ein gleiches oder kleineres Ergebnis hatten. In der Regel wird davon ausgegangen, dass Normwertskalen normalverteilt sind.

Normwerte als Schwellwerte

In der Medizin stellen die Normwerte häufig Grenzwerte dar, an denen abgelesen wird, ob ein Wert möglicherweise als pathologisch betrachtet wird oder nicht. Die Gewinnung der Normwerte geschieht auf dem gleichen Wege wie in der Psychologie: es wird eine ausreichend große Stichprobe der zu beschreibenden Grundgesamtheit untersucht. Als Normwertgrenzen werden hier meist die Werte eingesetzt, die die niedrigsten 2,5 % (Prozentrang 2,5 und niedriger) und die höchsten 2,5 % (Prozentrang 97,5 und höher) der untersuchten gesunden Personen erreichen. Hierbei muss jedoch ein Wert außerhalb der Norm nicht immer auch pathologisch sein. Er kann auch nur besonders gut sein oder eine Normvariante darstellen. In der Kinder- und Jugendmedizin werden für einige Bereiche die Grenzen bei PR 10 und PR 90 angesetzt, um zu prüfen, ob sich das Kind innerhalb eines Entwicklungs-Korridors befindet.

Siehe auch

• Normierung (Psychologische Diagnostik)

Literatur

• Markus Pospeschill: Empirische Methoden in der Psychologie. Band 4010. UTB, München 2013, ISBN 978-3-8252-4010-3. 
• Jürgen Bortz, Nicola Döring: Forschungsmethoden und Evaluation: für Human- und Sozialwissenschaftler. 4., überarb. Auflage. Springer, Berlin, Heidelberg 2006, ISBN 978-3-540-33305-0. 

Weblinks

• Normwert-Rechner zum Umrechnen verschiedener Normwert-Skalen