Normalverteilung
| Normalverteilung | |
Dichtefunktion 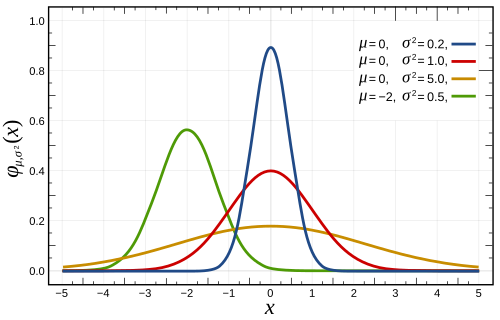 Dichtefunktionen der Normalverteilung : Dichtefunktionen der Normalverteilung :(blau), (rot), (gelb) und (grün) | |
Verteilungsfunktion Verteilungsfunktionen der Normalverteilungen: Verteilungsfunktionen der Normalverteilungen:(blau), (rot), (gelb) und (grün) | |
| Parameter | – Erwartungswert – Varianz |
|---|---|
| Träger | |
| Dichtefunktion | |
| Verteilungsfunktion | – mit Fehlerfunktion |
| Erwartungswert | |
| Median | |
| Modus | |
| Varianz | |
| Schiefe | |
| Wölbung | |
| Entropie | |
| Momenterzeugende Funktion | |
| Charakteristische Funktion | |
| Fisher-Information | |
Die Normal- oder Gauß-Verteilung (nach Carl Friedrich Gauß) ist in der Stochastik ein wichtiger Typ stetiger Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichtefunktion wird auch Gauß-Funktion, gaußsche Normalverteilung, gaußsche Verteilungskurve, Gauß-Kurve, gaußsche Glockenkurve, gaußsche Glockenfunktion, Gauß-Glocke oder schlicht Glockenkurve genannt. Sie hat die Form
mit dem Erwartungswert und der Standardabweichung .
Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen Grenzwertsatz, dem zufolge Verteilungen, die durch additive Überlagerung einer großen Zahl von unabhängigen Einflüssen entstehen, unter schwachen Voraussetzungen annähernd normalverteilt sind.
In der Messtechnik wird häufig eine Normalverteilung angesetzt, um die Streuung von Messwerten zu beschreiben. Die Abweichungen der Messwerte vieler natur-, wirtschafts- und ingenieurwissenschaftlicher Vorgänge vom Erwartungswert lassen sich durch die Normalverteilung in guter Näherung beschreiben (vor allem Prozesse, die in mehreren Faktoren unabhängig voneinander in verschiedene Richtungen wirken).
Zufallsvariablen mit Normalverteilung benutzt man zur Beschreibung zufälliger Vorgänge wie:
- zufällige Streuung von Messwerten,
- zufällige Abweichungen vom Sollmaß bei der Fertigung von Werkstücken,
- Beschreibung der brownschen Molekularbewegung.
Der Erwartungswert kann als Schwerpunkt der Verteilung interpretiert werden. Die Standardabweichung gibt ihre Breite an.
Geschichte
Im Jahre 1733 zeigte Abraham de Moivre in seiner Schrift The Doctrine of Chances im Zusammenhang mit seinen Arbeiten am Grenzwertsatz für Binomialverteilungen eine Abschätzung des Binomialkoeffizienten, die als Vorform der Normalverteilung gedeutet werden kann.[1]
Die für die Normierung der Normalverteilungsdichte zur Wahrscheinlichkeitsdichte notwendige Berechnung des nichtelementaren Integrals
gelang Pierre-Simon Laplace im Jahr 1782 (nach anderen Quellen Poisson).
Im Jahr 1809 publizierte Gauß sein Werk Theoria motus corporum coelestium in sectionibus conicis solem ambientium (deutsch Theorie der Bewegung der in Kegelschnitten sich um die Sonne bewegenden Himmelskörper), das neben der Methode der kleinsten Quadrate und der Maximum-Likelihood-Schätzung die Normalverteilung definiert. Wiederum Laplace war es, der 1810 den Satz vom zentralen Grenzwert bewies, der die Grundlage der theoretischen Bedeutung der Normalverteilung darstellt und de Moivres Arbeit am Grenzwertsatz für Binomialverteilungen abschloss.
Adolphe Quetelet erkannte schließlich bei Untersuchungen des Brustumfangs von mehreren tausend Soldaten im Jahr 1845 eine verblüffende Übereinstimmung mit der Normalverteilung und brachte die Normalverteilung in die angewandte Statistik.[2]
Zunächst wurde die Normalverteilung als Fehlergesetz (Law of Error) oder Fehlerkurve (error curve) bezeichnet. Die erste unzweideutige Verwendung der Bezeichnung „Normalverteilung“ für die Verteilung mit der Formulierung „Normal Curve of Distribution“ wird Francis Galton (1889)[3] zugeschrieben.[4][5] Der Wissenschaftshistoriker Stephen M. Stigler identifizierte[6] drei frühere – vermutlich voneinander unabhängige – Verwendungen des Wortes normal im Zusammenhang mit der später Normalverteilung genannten Verteilung durch Charles S. Peirce (1873),[7] Francis Galton (1877)[8] und Wilhelm Lexis (1877),[9] dabei werden eher die beobachteten Werte oder Teile der beobachteten Werte als „normal“ bezeichnet.
Definition
Eine Zufallsvariable hat eine Normalverteilung mit Erwartungswert und Standardabweichung bzw. Varianz , wobei , oft geschrieben als , wenn die folgende Wahrscheinlichkeitsdichte hat:[10][11]
- .
Eine Zufallsvariable, deren Wahrscheinlichkeitsverteilung eine Normalverteilung ist, heißt normalverteilt. Eine normalverteilte Zufallsvariable heißt auch gaußsche Zufallsvariable.
Eine Normalverteilung mit den Parametern und heißt Standardnormalverteilung, standardisierte Normalverteilung[12] oder normierte Normalverteilung.[13] Eine Zufallsvariable, deren Wahrscheinlichkeitsverteilung eine Standardnormalverteilung ist, heißt standardnormalverteilt. Eine standardnormalverteilte Zufallsvariable hat die Dichtefunktion
- ,
siehe auch Fehlerintegral.
Zur mehrdimensionalen Verallgemeinerung siehe Mehrdimensionale Normalverteilung.
Alternative Definition
Alternativ lässt sich die Normalverteilung auch über ihre charakteristische Funktion definieren:
Diese Definition erweitert die obige Definition zusätzlich um den Fall .
Eigenschaften
Erwartungswert und Varianz
Ist , dann gilt für den Erwartungswert
und für die Varianz
- .
Insbesondere ist der Erwartungswert der Standardnormalverteilung , denn für gilt
da der Integrand integrierbar und punktsymmetrisch ist.
Standardisierung
Eine Zufallsvariable wird durch Standardisierung in eine standardnormalverteilte Zufallsvariable überführt.
Verteilungsfunktion
Die Wahrscheinlichkeitsdichte einer normalverteilten Zufallsvariable ist nicht elementar integrierbar, sodass Wahrscheinlichkeiten numerisch berechnet werden müssen. Die Wahrscheinlichkeiten können mithilfe einer Standardnormalverteilungstabelle berechnet werden, die eine Standardform verwendet. Dabei bedient man sich der Tatsache, dass die lineare Transformation einer normalverteilten Zufallsvariablen zu einer neuen Zufallsvariable führt, die ebenfalls normalverteilt ist. Konkret heißt das, wenn und , wobei und Konstanten sind mit , dann gilt . Damit bilden Normalverteilungen eine Lage-Skalen-Familie.
Die Verteilungsfunktion der Normalverteilung ist durch
gegeben. Die Wahrscheinlichkeit, dass eine Realisierung im Intervall hat, ist damit .
Wenn man durch die Substitution statt eine neue Integrationsvariable einführt, ergibt sich mit und (gemäß dem oben angeführten Linearitätskriterium)
Dabei ist die Verteilungsfunktion der Standardnormalverteilung:
Mit der Fehlerfunktion lässt sich darstellen als
Funktionsgraph
Der Graph der Dichtefunktion bildet eine Gaußsche Glockenkurve und ist achsensymmetrisch mit dem Parameter als Symmetriezentrum, der auch den Erwartungswert, den Median und den Modus der Verteilung darstellt. Vom zweiten Parameter hängen Höhe und Breite der Wahrscheinlichkeitsdichte ab, die Wendepunkte liegen bei .
Der Graph der Verteilungsfunktion ist punktsymmetrisch zum Punkt Für gilt insbesondere und für alle .
Als Wahrscheinlichkeitsverteilung ist die Gesamtfläche unter der Kurve gleich . Dass jede Normalverteilung normiert ist, ergibt sich über die lineare Substitution :
- .
Für die Normiertheit des letzteren Integrals siehe Fehlerintegral.
Momenterzeugende Funktion und höhere Momente
Die momenterzeugende Funktion der -verteilten Normalverteilung lautet
- .
Nach dem stochastischen Moment 1. Ordnung, dem Erwartungswert, und dem zentralen Moment 2. Ordnung, der Varianz, ist die Schiefe das zentrale Moment 3. Ordnung. Es ist unabhängig von den Parametern und immer den Wert . Die Wölbung als zentrales Moment 4. Ordnung ist ebenfalls von und unabhängig und ist gleich . Um die Wölbungen anderer Verteilungen besser einschätzen zu können, werden sie oft mit der Wölbung der Normalverteilung verglichen. Dabei wird die Wölbung der Normalverteilung auf normiert (Subtraktion von 3); diese Größe wird als Exzess bezeichnet.
Die ersten Momente wie sind folgt:
| Ordnung | Moment | zentrales Moment |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
Alle zentralen Momente lassen sich durch die Standardabweichung darstellen:
dabei wurde die Doppelfakultät verwendet:
Auch für kann eine Formel für nicht-zentrale Momente angegeben werden. Dafür transformiert man und wendet den binomischen Lehrsatz an.
Die mittlere absolute Abweichung ist und der Interquartilsabstand .
Standardabweichung

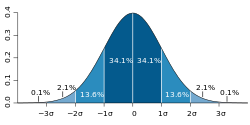
Aus der Standardnormalverteilungstabelle ist ersichtlich, dass für normalverteilte Zufallsvariablen jeweils ungefähr
- 68,3 % der Realisierungen im Intervall ,
- 95,4 % im Intervall und
- 99,7 % im Intervall
- 95,4 % im Intervall und
liegen. Da in der Praxis viele Zufallsvariablen annähernd normalverteilt sind, werden diese Werte aus der Normalverteilung oft als Faustformel benutzt. So wird beispielsweise oft als die halbe Breite des Intervalls angenommen, das die mittleren zwei Drittel der Werte in einer Stichprobe umfasst.
Realisierungen außerhalb der zwei- bis dreifachen Standardabweichung gelten oft als verdächtig, Ausreißer zu sein. Sie können ein Hinweis auf grobe Fehler der Datenerfassung oder auch auf das Nichtvorhandensein einer Normalverteilung sein. Andererseits liegt bei einer Normalverteilung im Durchschnitt ca. jeder 20. Messwert außerhalb der zweifachen Standardabweichung und ca. jeder 370. Messwert außerhalb der dreifachen Standardabweichung, ohne dass es sich dabei um Ausreißer handelt.


Die Wahrscheinlichkeit, dass eine normalverteilte Zufallsvariable einen Wert im Intervall annimmt, ist genau so groß, wie die Wahrscheinlichkeit, dass ein standardnormalverteilte Zufallsvariable einen Wert im Intervall annimmt, es gilt also
- .[14]
Damit können bestimmte Wahrscheinlichkeitsaussagen für Normalverteilungen mit beliebigen Parametern und auf die Standardnormalverteilung zurückgeführt werden.
Die Wahrscheinlichkeit kann alternativ durch die Verteilungsfunktion der Standardnormalverteilung oder durch die Fehlerfunktion ausgedrückt werden:
Umgekehrt ist zu einer vorgegebenen Wahrscheinlichkeit die Stelle , für die gilt, durch
gegeben.
| 0,674490 | 50 % | 50 % |
| 1 | 68,268 9492 % | 31,731 0508 % |
| 1,17741 (Halbwertsbreite) | 76,096 8106 % | 23,903 1891 % |
| 1,644854 | 90 % | 10 % |
| 2 | 95,449 9736 % | 4,550 0264 % |
| 2,575829 | 99 % | 1 % |
| 3 | 99,730 0204 % | 0,269 9796 % |
| 3,290527 | 99,9 % | 0,1 % |
| 3,890592 | 99,99 % | 0,01 % |
| 4 | 99,993 666 % | 0,006 334 % |
| 4,417173 | 99,999 % | 0,001 % |
| 4,891638 | 99,9999 % | 0,0001 % |
| 5 | 99,999 942 6697 % | 0,000 057 3303 % |
| 5,326724 | 99,999 99 % | 0,000 01 % |
| 5,730729 | 99,999 999 % | 0,000 001 % |
| 6 | 99,999 999 8027 % | 0,000 000 1973 % |
Halbwertsbreite
Der Wert der Dichtefunktion der Standardnormalverteilung fällt auf die Hälfte des Maximums, wenn , also bei . Die Halbwertsbreite ist damit das fache der Standardabweichung.
Variationskoeffizient
Aus Erwartungswert und Standardabweichung der -Verteilung erhält man unmittelbar den Variationskoeffizienten
Kumulanten
Die kumulantenerzeugende Funktion ist
Damit ist die erste Kumulante , die zweite ist und alle weiteren Kumulanten verschwinden.
Charakteristische Funktion
Die charakteristische Funktion für eine standardnormalverteilte Zufallsvariable ist
- .
Für eine Zufallsvariable erhält man daraus mit :
- .
Invarianz gegenüber Faltung
Die Normalverteilung ist invariant gegenüber der Faltung, d. h., die Summe unabhängiger normalverteilter Zufallsvariablen ist wieder normalverteilt (siehe dazu auch unter stabile Verteilungen bzw. unter unendliche teilbare Verteilungen). Somit bildet die Normalverteilung eine Faltungshalbgruppe in ihren beiden Parametern. Eine veranschaulichende Formulierung dieses Sachverhaltes lautet: Die Faltung einer Gaußkurve der Standardabweichung mit einer Gaußkurve der Standardabweichung ergibt wieder eine Gaußkurve mit der Standardabweichung
- .
Sind also zwei unabhängige Zufallsvariablen mit
so ist deren Summe ebenfalls normalverteilt:
- .
Das kann beispielsweise mit Hilfe von charakteristischen Funktionen gezeigt werden, indem man verwendet, dass die charakteristische Funktion der Summe das Produkt der charakteristischen Funktionen der Summanden ist (vgl. Faltungssatz der Fouriertransformation).
Damit ist jede Linearkombination wieder normalverteilt. Nach dem Satz von Cramér gilt sogar die Umkehrung: Ist eine normalverteilte Zufallsvariable die Summe von unabhängigen Zufallsvariablen, dann sind die Summanden ebenfalls normalverteilt. Man spricht davon, dass die Normalverteilung reproduktiv ist bzw. die Reproduktivitätseigenschaft besitzt.
Die Dichtefunktion der Normalverteilung ist ein Fixpunkt der Fourier-Transformation, d. h., die Fourier-Transformierte einer Gaußkurve ist wieder eine Gaußkurve. Das Produkt der Standardabweichungen dieser korrespondierenden Gaußkurven ist konstant; es gilt die Heisenbergsche Unschärferelation.
Entropie
Eine normalverteilte Zufallsvariable hat die Shannon-Entropie .[16][17] Sie hat für gegebenen Erwartungswert und gegebene Varianz die größte Entropie unter allen stetigen Verteilungen.[18]
Anwendung
Beispiel zur Standardabweichung
Die Körpergröße des Menschen ist näherungsweise normalverteilt. Bei einer Stichprobe von 1.284 Mädchen und 1.063 Jungen zwischen 14 und 18 Jahren wurde bei den Mädchen eine durchschnittliche Körpergröße von 166,3 cm (Standardabweichung 6,39 cm) und bei den Jungen eine durchschnittliche Körpergröße von 176,8 cm (Standardabweichung 7,46 cm) gemessen.[19]
Demnach lässt obige Schwankungsbreite erwarten, dass 68,3 % der Mädchen eine Körpergröße im Bereich 166,3 cm ± 6,39 cm und 95,4 % im Bereich 166,3 cm ± 12,8 cm haben, also
- 16 % [≈ (100 % − 68,3 %)/2] der Mädchen kleiner als 160 cm (und 16 % entsprechend größer als 173 cm) sind und
- 2,5 % [≈ (100 % − 95,4 %)/2] der Mädchen kleiner als 154 cm (und 2,5 % entsprechend größer als 179 cm) sind.
Für die Jungen lässt sich erwarten, dass 68,3 % eine Körpergröße im Bereich 176,8 cm ± 7,46 cm und 95,4 % im Bereich 176,8 cm ± 14,92 cm haben, also
- 16 % der Jungen kleiner als 169 cm (und 16 % größer als 184 cm) und
- 2,5 % der Jungen kleiner als 162 cm (und 2,5 % größer als 192 cm) sind.
Kontaminierte Normalverteilung

Von der Verteilung
ist die Standardabweichung . Die Verteilung ist optisch kaum von der Normalverteilung zu unterscheiden (siehe Bild), aber bei ihr liegen im Intervall 92,5 % der Werte. Solche kontaminierten Normalverteilungen sind in der Praxis häufig; das genannte Beispiel beschreibt die Situation, wenn zehn Präzisionsmaschinen etwas herstellen, aber eine davon schlecht justiert ist und mit zehnmal so hohen Abweichungen wie die anderen neun produziert.
Gestutzte Normalverteilung
Bei der gestutzten Normalverteilung ist die Wahrscheinlichkeitsdichte außerhalb eines Intervalls mit gleich Null. Entsprechend erhöht sich in dem Intervall, so dass das Integral bleibt.
Six Sigma
Da der Anteil der Werte außerhalb der sechsfachen Standardabweichung mit ca. 2 ppb verschwindend klein wird, gilt ein solches Intervall als gutes Maß für eine nahezu vollständige Abdeckung aller Werte. Das wird im Qualitätsmanagement durch die Methode Six Sigma genutzt, indem die Prozessanforderungen Toleranzgrenzen von mindestens vorschreiben. Allerdings geht man dort von einer langfristigen Erwartungswertverschiebung um 1,5 Standardabweichungen aus, sodass der zulässige Fehleranteil auf 3,4 ppm steigt. Dieser Fehleranteil entspricht einer viereinhalbfachen Standardabweichung (). Ein weiteres Problem der -Methode ist, dass die -Punkte praktisch nicht bestimmbar sind. Bei unbekannter Verteilung (d. h., wenn es sich nicht ganz sicher um eine Normalverteilung handelt) grenzen zum Beispiel die Extremwerte von 1.400.000.000 Messungen ein 75-%-Konfidenzintervall für die -Punkte ein.[20]
Beziehungen zu anderen Verteilungsfunktionen
Normalverteilung als Grenzverteilung der Binomialverteilung
Die Binomialverteilung ist eine diskrete Verteilung, die sich aus einer Anzahl an Versuchen ergibt. Jeder einzelne Versuch hat die Wahrscheinlichkeit eines Erfolges . Die Binomialverteilung gibt dann die Wahrscheinlichkeit an, dass die Versuche genau -mal ein Erfolg war, mit .
Durch einen Grenzübergang für ergeben sich die Dichtefunktion einer Normalverteilung aus der Wahrscheinlichkeitsfunktion der Binomialverteilung (lokaler Grenzwertsatz von Moivre-Laplace) und die Verteilungsfunktion einer Normalverteilung aus der Verteilungsfunktion der Binomialverteilung (globaler Grenzwertsatz von Moivre-Laplace). Dies ist eine Rechtfertigung dafür, die Binomialverteilung mit den Parametern und für hinreichend große durch die Normalverteilung zu approximieren.
Approximation der Binomialverteilung durch die Normalverteilung
Die Normalverteilung kann zur Approximation der Binomialverteilung verwendet werden, wenn der Stichprobenumfang hinreichend groß und in der Grundgesamtheit der Anteil der gesuchten Eigenschaft weder zu groß noch zu klein ist (Satz von Moivre-Laplace, zentraler Grenzwertsatz, zur experimentellen Bestätigung siehe auch unter Galtonbrett).
Ist ein Bernoulli-Versuch mit voneinander unabhängigen Stufen (bzw. Zufallsexperimenten) mit einer Erfolgswahrscheinlichkeit gegeben, so lässt sich die Wahrscheinlichkeit für Erfolge allgemein durch berechnen (Binomialverteilung).
Diese Binomialverteilung kann durch eine Normalverteilung approximiert werden, wenn hinreichend groß und weder zu groß noch zu klein ist. Als Faustregel dafür gilt . Für den Erwartungswert und die Standardabweichung gilt dann:
- und .
Damit gilt für die Standardabweichung .
Falls diese Bedingung nicht erfüllt sein sollte, ist die Ungenauigkeit der Näherung immer noch vertretbar, wenn gilt: und zugleich .
Folgende Näherung ist dann brauchbar:
Bei der Normalverteilung wird die untere Grenze um 0,5 verkleinert und die obere Grenze um 0,5 vergrößert, um eine bessere Approximation gewährleisten zu können. Dies nennt man auch „Stetigkeitskorrektur“. Nur wenn einen sehr hohen Wert besitzt, kann auf sie verzichtet werden.
Da die Binomialverteilung diskret ist, muss auf einige Punkte beim Rechnen mit einer binomialverteilten Zufallsvariablen geachtet werden:
- Der Unterschied zwischen oder (sowie zwischen größer und größer gleich) muss beachtet werden (was ja bei der Normalverteilung nicht der Fall ist). Deshalb muss bei die nächstkleinere natürliche Zahl gewählt werden, d. h.
- bzw. ,
- damit mit der Normalverteilung weitergerechnet werden kann.
- Zum Beispiel:
- Außerdem ist
- (unbedingt mit Stetigkeitskorrektur)
- und lässt sich somit durch die oben angegebene Formel berechnen.
Der große Vorteil der Approximation liegt darin, dass sehr viele Stufen einer Binomialverteilung sehr schnell und einfach bestimmt werden können.
Beziehung zur Cauchy-Verteilung
Der Quotient von zwei stochastisch unabhängigen -standardnormalverteilten Zufallsvariablen ist Cauchy-verteilt.
Beziehung zur Chi-Quadrat-Verteilung
Das Quadrat einer standardnormalverteilten Zufallsvariablen hat eine Chi-Quadrat-Verteilung mit einem Freiheitsgrad. Also: Wenn , dann . Weiterhin gilt: Wenn gemeinsam stochastisch unabhängige Chi-Quadrat-verteilte Zufallsvariablen sind, dann gilt
- .
Daraus folgt mit unabhängig und standardnormalverteilten Zufallsvariablen :[21]
Weitere Beziehungen sind:
- Die Summe mit und unabhängigen normalverteilten Zufallsvariablen genügt einer Chi-Quadrat-Verteilung mit Freiheitsgraden.
- Mit steigender Anzahl an Freiheitsgraden (df ≫ 100) nähert sich die Chi-Quadrat-Verteilung der Normalverteilung an.
- Die Chi-Quadrat-Verteilung wird zur Konfidenzschätzung für die Varianz einer normalverteilten Grundgesamtheit verwendet.
Beziehung zur Rayleigh-Verteilung
Der Betrag zweier unabhängiger normalverteilter Zufallsvariablen , jeweils mit Mittelwert und gleichen Varianzen , ist Rayleigh-verteilt mit Parameter .
Beziehung zur logarithmischen Normalverteilung
Ist die Zufallsvariable normalverteilt mit , dann ist die Zufallsvariable logarithmisch-normalverteilt, also .
Die Entstehung einer logarithmischen Normalverteilung ist auf multiplikatives, die einer Normalverteilung auf additives Zusammenwirken vieler Zufallsvariablen zurückführen.
Beziehung zur F-Verteilung
Wenn die stochastisch unabhängigen und normalverteilten Zufallsvariablen und die Parameter
und
besitzen, dann unterliegt die Zufallsvariable
einer F-Verteilung mit Freiheitsgraden. Dabei sind
- .
Beziehung zur studentschen t-Verteilung
Wenn die stochastisch unabhängigen Zufallsvariablen identisch normalverteilt sind mit den Parametern und , dann unterliegt die stetige Zufallsvariable
mit dem Stichprobenmittel , der Stichprobenvarianz und einer studentschen t-Verteilung mit Freiheitsgraden.
Für eine zunehmende Anzahl an Freiheitsgraden nähert sich die studentsche t-Verteilung der Normalverteilung immer näher an. Als Faustregel gilt, dass man ab ca. die studentsche t-Verteilung bei Bedarf durch die Normalverteilung approximieren kann.
Die studentsche t-Verteilung wird zur Konfidenzschätzung für den Erwartungswert einer normalverteilten Zufallsvariable bei unbekannter Varianz verwendet.
Testen auf Normalverteilung


Um zu überprüfen, ob vorliegende Daten normalverteilt sind, können unter anderen folgende Methoden und Tests angewandt werden:
- Chi-Quadrat-Test
- Kolmogorow-Smirnow-Test
- Anderson-Darling-Test (Modifikation des Kolmogorow-Smirnow-Tests)
- Lilliefors-Test (Modifikation des Kolmogorow-Smirnow-Tests)
- Cramér-von-Mises-Test
- Shapiro-Wilk-Test
- Jarque-Bera-Test
- Q-Q-Plot (deskriptive Überprüfung)
- Maximum-Likelihood-Methode (deskriptive Überprüfung)
Die Tests haben unterschiedliche Eigenschaften hinsichtlich der Art der Abweichungen von der Normalverteilung, die sie erkennen. So erkennt der Kolmogorov-Smirnov-Test Abweichungen in der Mitte der Verteilung eher als Abweichungen an den Rändern, während der Jarque-Bera-Test ziemlich sensibel auf stark abweichende Einzelwerte an den Rändern („schwere Ränder“) reagiert.
Beim Lilliefors-Test muss im Gegensatz zum Kolmogorov-Smirnov-Test nicht standardisiert werden, d. h., und der angenommenen Normalverteilung dürfen unbekannt sein.
Mit Hilfe von Quantil-Quantil-Diagrammen bzw. Normal-Quantil-Diagrammen ist eine einfache grafische Überprüfung auf Normalverteilung möglich.
Mit der Maximum-Likelihood-Methode können die Parameter und der Normalverteilung geschätzt und die empirischen Daten mit der angepassten Normalverteilung grafisch verglichen werden.
Erzeugung normalverteilter Zufallszahlen
Alle folgenden Verfahren erzeugen standardnormalverteilte Zufallszahlen. Durch lineare Transformation lassen sich hieraus beliebige normalverteilte Zufallszahlen erzeugen: Ist die Zufallsvariable -verteilt, so ist schließlich -verteilt.
Box-Muller-Methode
Nach der Box-Muller-Methode lassen sich zwei unabhängige, standardnormalverteilte Zufallsvariablen und aus zwei unabhängigen, gleichverteilten Zufallsvariablen , sogenannten Standardzufallszahlen, simulieren:
und
Polar-Methode
Die Polar-Methode von George Marsaglia ist auf einem Computer schneller, da sie keine Auswertungen von trigonometrischen Funktionen benötigt:
- Erzeuge zwei voneinander unabhängige, im Intervall gleichverteilte Zufallszahlen und
- Berechne . Falls oder , gehe zurück zu Schritt 1.
- Berechne .
- für liefert zwei voneinander unabhängige, standardnormalverteilte Zufallszahlen und .
Ziggurat-Algorithmus
Der Ziggurat-Algorithmus, der ebenfalls von George Marsaglia entwickelt wurde, ist effizienter als die Box-Muller-Methode.[22] Er ist der voreingestellte Algorithmus, mit dem in Matlab und Octave normalverteilte Zufallszahlen erzeugt werden.[23][24]
Verwerfungsmethode
Normalverteilungen lassen sich mit der Verwerfungsmethode (siehe dort) simulieren.
Inversionsmethode
Die Normalverteilung lässt sich auch mit der Inversionsmethode berechnen.
Mit der -gleichverteilten Verteilung wird über die Inverse Verteilungsfunktion die Standardnormalverteilung erzeugt:
Da die inverse Verteilungsfunktion nicht explizit mit elementaren Funktionen darstellbar ist, muss man auf eine komplexere numerische Darstellung zurückgreifen, mit relativ hohem Aufwand. Reihenentwicklungen sind in der Literatur zu finden.[25]
Zwölferregel
Die Zwölferregel liefert keine exakte Normalverteilung, diese wird nur genähert. Der zentrale Grenzwertsatz besagt, dass sich unter bestimmten Voraussetzungen die Verteilung der Summe unabhängig und identisch verteilter Zufallszahlen einer Normalverteilung nähert.
Nach der Zwölferregel wird die Standardnormalverteilung durch die Verteilung der Zufallsvariablen approximiert, wobei die Summe von zwölf stochastisch unabhängigen, im Intervall [0,1] gleichverteilten Zufallszahlen ist. Der Erwartungswert von ist 6 und die Varianz von ist 1, sodass die Zufallsvariable den Erwartungswert 0 und die Varianz 1 hat. Dies führt für viele Anwendungen zu einer akzeptablen Approximation einer Standardnormalverteilung durch die Verteilung der Zufallsvariablen . Das Verfahren ist allerdings weder effizient noch wird eine echte Normalverteilung erreicht.
Zudem ist die geforderte Unabhängigkeit der zwölf Zufallsvariablen bei den immer noch häufig verwendeten Linearen Kongruenzgeneratoren (LKG) nicht garantiert. Im Gegenteil wird vom Spektraltest für LKG meist nur die Unabhängigkeit von maximal vier bis sieben der garantiert. Für numerische Simulationen ist die Zwölferregel daher sehr bedenklich und sollte, wenn überhaupt, dann ausschließlich mit aufwändigeren, aber besseren Pseudo-Zufallsgeneratoren wie z. B. dem Mersenne-Twister (Standard in Python, GNU R) oder WELL genutzt werden. Andere, sogar leichter zu programmierende Verfahren sind daher der Zwölferregel vorzuziehen.
Anwendungen außerhalb der Wahrscheinlichkeitsrechnung
In der Statistik ist die Normalverteilung eine wichtige Wahrscheinlichkeitsverteilung. Sie wird verwendet zur Modellierung einer Merkmalsverteilung in der Grundgesamtheit und zur Modellierung der Verteilung von Messfehlern. Außerdem entsteht sie als asymptotische Verteilung von Schätzfunktionen und allgemeineren Statistiken, siehe dazu zentrale Grenzwertsätze der Statistik.
Die Normalverteilung lässt sich auch zur Beschreibung nicht direkt stochastischer Sachverhalte verwenden, etwa in der Physik für das Amplitudenprofil der Gauß-Strahlen und andere Verteilungsprofile.
Zudem findet sie Verwendung in der Gabor-Transformation im Bereich der Signal- und Bildbearbeitung.
Siehe auch
Literatur
- Catherine Forbes, Merran Evans, Nicholas Hastings, Brain Peacock (Hrsg.): Statistical Distributions. 4. Auflage. Wiley & Sons, Hoboken 2011, ISBN 978-0-470-39063-4, Kap. 33: Normal (Gaussian) Distribution, S. 143–148.
- P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, Normalverteilung, S. 288–290.
- Horst Rinne: Taschenbuch der Statistik. 4. Auflage. Harri Deutsch, Frankfurt am Main 2008, ISBN 978-3-8171-1827-4, Teil B, Kap. 3.10.1: Eindimensionale Normalverteilung, S. 298–306.
- Jagdish K. Patel, Campbell R. Read: Handbook of the Normal Distribution (= Statistics:Textbooks and Monographs). Second edition, revised and expanded Auflage. Dekker, New York / Basel / Hong Kong 1966, ISBN 0-8247-9342-0.
- Stephen M. Stigler: The history of statistics: the measurement of uncertainty before 1900. Belknap Series. Harvard University Press, 1986. ISBN 978-0-674-40341-3.
- Paul J. Nahin: The Probability Integral. Its Origin, Its Importance, and Its Calculation. Springer, Cham 2023, ISBN 978-3-03138415-8.
Weblinks
- Anschauliche Erklärung der Normalverteilung mit interaktivem Graphen
- Darstellung mit Programmcode ( vom 7. Februar 2018 im Internet Archive) in Visual Basic Classic
- Online-Rechner Normalverteilung
- Santa Cruz Institute for Particle Physics: The Normal Approximation to the Binomial Distribution
- University of Connecticut: Normal approximation to the binomial
- Universität Uppsala: Approximating the Binomial Distribution by the Normal Distribution – Error and Accuracy
- University of Saskatchewan: The Normal Distribution as a Limit of Binomial Distributions
Einzelnachweise
- ↑ Wolfgang Götze, Christel Deutschmann, Heike Link: Statistik. Lehr- und Übungsbuch mit Beispielen aus der Tourismus- und Verkehrswirtschaft. Oldenbourg, München 2002, ISBN 3-486-27233-0, S. 170 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Sur l'appréciation des documents statistiques, et en particulier sur l'appréciation des moyennes. In: Bulletin de la Commission Centrale des Statistique. Band 2, 1845, S. 205–286 (google.be).
- ↑ Francis Galton: Natural Inheritance. Macmillan, London 1889, S. 51, Normal Curve of Distribution.
- ↑ Herbert A. David: First (?) Occurence of Common Terms in Mathematical Statistics. In: The American Statistician. Band 49, Nr. 2, 1995, S. 121–133, JSTOR:2684625.
- ↑ Jeff Miller: Earliest Known Uses of Some of the Words of Probability & Statistics. Abgerufen am 27. September 2023.
- ↑ Stephen M. Stigler: Statistics on the Table. The History of Statistical Concepts and Methods. Harvard University Press, Cambridge / London 1999, ISBN 0-674-00979-7.
- ↑ Charles S. Peirce: On the theory of errors of observations. In: Report of the Superintendent of the U. S. Coast Survey for the Year Ending June 1870, Appendix no. 21. S. 200–224 (Wiederabgedruckt in S. M. Stigler (Hrsg.), American Contributions to Mathematical Statistics in the Ninteenth Century, 2 Bände. Arno Press, New York 1980).
- ↑ Francis Galton: Typical laws of heredity. In: Nature. Band 15, 1877, S. 492–495, 512–514, 532–533 (Auch publiziert in Proceedings of the Royal Institution of Great Britain. Band 8, 1877, S. 282–301).
- ↑ Wilhelm Lexis: Zur Theorie der Massenerscheinungen in der menschlichen Gesellschaft. Fr. Wagner’sche Buchhandlung, Freiburg i. B. 1877 (utlib.ee [PDF]).
- ↑ Bronstein: Taschenbuch der Mathematik. Kap. 16, Wahrscheinlichkeitsrechnung und mathematische Statistik.
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. 1988, S. 47.
- ↑ P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, Normalveretilung, S. 289.
- ↑ Bronstein: Taschenbuch der Mathematik. Kap. 16, Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Harri Deutsch Verlag, 2000, ISBN 3-8171-2005-2, S. 779.
- ↑ Es gilt
- ↑ Es gilt
- ↑ Horst Rinne: Taschenbuch der Statistik. 2008, S. 302.
- ↑ Catherine Forbes et al. (Hrsg.): Statistical Distributions. 2011, S. 144.
- ↑ P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, Entropie einer Zufallsgröße, S. 86.
- ↑ Mareke Arends: Epidemiologie bulimischer Symptomatik unter 10-Klässlern in der Stadt Halle. Dissertation. Martin-Luther-Universität Halle-Wittenberg, 2005, Tabelle 9, S. 30. urn:nbn:de:gbv:3-000008151
- ↑ H. Schmid, A. Huber: Measuring a Small Number of Samples and the 3σ Fallacy. (PDF; 1,6 MB) In: IEEE Solid-State Circuits Magazine, Band 6, Nr. 2, 2014, S. 52–58, doi:10.1109/MSSC.2014.2313714.
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. 1988, S. 49.
- ↑ Michael Günther, Ansgar Jüngel: Finanzderivate mit MATLAB - Mathematische Modellierung und numerische Simulation. Vieweg+Teubner Verlag, 2003, ISBN 978-3-8348-0879-0, S. 115.
- ↑ Creating and Controlling a Random Number Stream in Matlab. Abgerufen am 16. September 2023.
- ↑ Octave Function Reference: randn. Abgerufen am 16. September 2023.
- ↑ William B. Jones, W. J. Thron: Continued Fractions: Analytic Theory and Applications. Addison-Wesley, 1980.
Auf dieser Seite verwendete Medien
Autor/Urheber: MartinThoma, Lizenz: CC0
Eine Auswahl an Verteilungsfunktionen der Normalverteilung mit
A selection of Normal Distribution Probability Density Functions (PDFs). Both the mean, μ, and variance, σ², are varied. The key is given on the graph.
Autor/Urheber: Moritz Kohls, Lizenz: CC BY 4.0
Eine χ²-verteilte Zufallsvariable mit 5 Freiheitsgraden wird auf Normalverteilung getestet. Für jeden Stichprobenumfang werden jeweils 10 000 einzelne Stichproben simuliert und 5 Anpassungstests zu einem Niveau von 5% durchgeführt.
Autor/Urheber: M.J., Lizenz: CC BY-SA 4.0
% GNU Octave source code
z=0:0.02:6.2;
zm=1:6;
zd=erfinv(1-10.^(-9:-1))*sqrt(2);
semilogy(z,1-erf(z/sqrt(2)),'-','linewidth',2)
hold on
plot(zm,1-erf(zm/sqrt(2)),'.','MarkerSize',12)
plot(zd,1-erf(zd/sqrt(2)),'.','MarkerSize',12)
hold off
grid on
set(gca,'yminorgrid','off')
axis tight
xlabel 'z'
ylabel 'Anteil außerhalb [-z, z]'
set(gca,'fontsize',20)
Autor/Urheber: Hanspi, Lizenz: CC BY-SA 4.0
Normalverteilung (a) und kontaminierte Normalverteilung (b)
Autor/Urheber: M. W. Toews, Lizenz: CC BY 2.5
Normal distribution curve that illustrates standard deviations. Each band has 1 standard deviation, and the labels indicate the approximate proportion of area (note: these add up to 99.8%, and not 100% because of rounding for presentation.)
Autor/Urheber: René Schwarz, Lizenz: CC BY-SA 3.0
Gegenüberstellende Visualisierung der Quantile einer Normalverteilung und einer Chi-Quadrat-Verteilung mit drei Freiheitsgraden.
Autor/Urheber: T.seppelt, Lizenz: CC BY-SA 3.0
Wahrscheinlichkeit p eines Konfidenzintervalls von z*Standardabweichung.