Metrische absolute Geometrie

Die metrische absolute Geometrie ist eine axiomatische Beschreibung der absoluten Geometrie, die ein gemeinsames Fundament für Modelle der euklidischen Geometrie und der nichteuklidischen Geometrie, konkret für elliptische Geometrien und hyperbolische Geometrien legt. Der Begriff und die Axiome stammen^[1] von Friedrich Bachmann, der sie in seinem Lehrbuch „Aufbau der Geometrie aus dem Spiegelungsbegriff“ formuliert, wichtige Folgerungen beweist und zeigt, wie die zweidimensionalen, metrischen absoluten Geometrien, die metrischen Ebenen in projektive Ebenen eingebettet werden können.^[2] Jede metrische Ebene bestimmt durch ihre „Metrik“ eine bestimmte Untergruppe der Projektivitätengruppe des zweidimensionalen projektiven Raumes ${\displaystyle \mathbb {P} ^{2}(K)}$, in den sie sich einbetten lässt, auch der Körper ${\displaystyle K}$ ist durch die metrische Ebene eindeutig bestimmt.

Es ist zu beachten, dass der Begriff „Metrik“ wie er in diesem Zusammenhang benutzt wird, nur entfernte, formale Ähnlichkeiten mit der Metrik eines metrischen Raumes hat. Die „Metrik“ bestimmt hier eine Orthogonalität zwischen Geraden, im Allgemeinen keinen Abstand zwischen Punkten. Man kann diese Orthogonalität in dem Koordinatenvektorraum, ${\displaystyle K^{3}}$ des projektiven Raumes ${\displaystyle \mathbb {P} ^{2}(K)}$, in den die metrische Ebene eingebettet wird, durch eine symmetrische Bilinearform beschreiben (zu dieser Beschreibung siehe Projektiv-metrische Geometrie). Diese Rechtwinkeldefinition entspricht dann formal der für den reellen, euklidischen Fall gewohnten Definition durch ein Skalarprodukt, also durch eine positiv-definite symmetrische Bilinearform.

Dieser Artikel beschreibt hauptsächlich die ebene metrische absolute Geometrie, ihre Modelle heißen metrische Ebenen.

Axiome der ebenen metrischen Geometrie

Das geometrisch formulierte Axiomensystem ist äquivalent zu dem gruppentheoretisch formulierten.^[3] In der metrischen Geometrie wird das gruppentheoretisch formulierte Axiomensystem zur Grundlage gemacht, aus diesem System wird geschlossen. Das geometrische Axiomensystem wird hier zum Abgleich mit anderen Axiomensystemen der absoluten Geometrie zitiert:

Geometrische Formulierung der Axiome

Gegeben sei ${\displaystyle ({\mathfrak {P}},{\mathfrak {S}},I,\perp )}$, wobei die Elemente der Menge ${\displaystyle {\mathfrak {P}}}$ Punkte, die Elemente der Menge ${\displaystyle {\mathfrak {S}}}$ Geraden genannt werden. ${\displaystyle I\subseteq ({\mathfrak {P}}\times {\mathfrak {S}})\cup ({\mathfrak {S}}\times {\mathfrak {P}})\;}$, die Inzidenzrelation sei eine zweistellige symmetrische Relation. Gilt ${\displaystyle PIg}$, so sagt man „${\displaystyle P}$ inzidiert mit ${\displaystyle g}$“ und verwendet dafür auch die sonst in der Geometrie üblichen Formulierungen. Kurz: ${\displaystyle ({\mathfrak {P}},{\mathfrak {S}},I)}$ ist eine (einfache) Inzidenzstruktur, wobei nicht gefordert wird, dass Punkt- und Geradenmenge disjunkt sind.^[4] Die Relation ${\displaystyle \perp \subseteq {\mathfrak {S}}\times {\mathfrak {S}}}$, die Orthogonalität, kann nur zwischen Geraden bestehen, man sagt dann für ${\displaystyle g\perp h}$: ${\displaystyle g}$ ist senkrecht zu ${\displaystyle h}$, ${\displaystyle g}$ ist ein Lot von ${\displaystyle h}$ usw.

Jede bijektive Selbstabbildung der Punktmenge ${\displaystyle {\mathfrak {P}}}$, bei der die Inzidenz und die Orthogonalität erhalten bleiben, heißt orthogonale Kollineation. Eine involutorische orthogonale Kollineation, die eine Gerade ${\displaystyle g\in {\mathfrak {S}}}$ punktweise fest lässt, heißt eine Spiegelung an der Geraden ${\displaystyle g}$.

1. Inzidenzaxiome: Es gibt wenigstens eine Gerade und mit jeder Geraden inzidieren wenigstens drei Punkte. Zu zwei verschiedenen Punkten gibt es genau eine^[5] Gerade, welche mit beiden Punkten inzidiert.
2. Orthogonalitätsaxiome: Ist ${\displaystyle a}$ senkrecht zu ${\displaystyle b}$, dann ist ${\displaystyle b}$ senkrecht zu ${\displaystyle a}$ (Symmetrie). Senkrechte Geraden haben einen Punkt gemein. Durch jeden Punkt gibt es zu jeder Geraden eine Senkrechte, und, falls der Punkt mit der Geraden inzidiert, nur eine.
3. An jeder Geraden gibt es wenigstens eine Spiegelung (Spiegelungsaxiom). Die Komposition von Spiegelungen an drei Geraden ${\displaystyle a,b,c}$, welche einen Punkt oder ein Lot gemeinsam haben, stimmt mit einer Spiegelung an einer Geraden ${\displaystyle d}$ überein (Satz von den drei Spiegelungen).

Gruppentheoretische Begriffe und Vereinbarungen

Die Verknüpfung einer Gruppe ${\displaystyle (G,\cdot )}$ wird multiplikativ oder häufiger durch Juxtaposition geschrieben, ${\displaystyle 1}$ ist ihr neutrales Element. Die Konjugation operiert wie das Potenzieren von rechts und ist dementsprechend definiert:

• ${\displaystyle \sigma ^{\alpha }:=\alpha ^{-1}\sigma \alpha \;}$, damit ist ${\displaystyle \sigma ^{\alpha \beta }=(\sigma ^{\alpha })^{\beta }}$
• Eine Teilmenge einer Gruppe heißt invariant, wenn sie dies unter der Konjugation ist. Eine Teilmenge ${\displaystyle M\subseteq G}$ ist also genau dann invariant, wenn für jedes Element ${\displaystyle \mu \in M}$ und jedes Gruppenelement ${\displaystyle \gamma \in G}$ stets ${\displaystyle \mu ^{\gamma }\in M}$ gilt.
• In einer Gruppe heißen die Elemente der Ordnung ${\displaystyle 2}$ involutorisch, damit ist insbesondere das neutrale Element der Gruppe keine Involution!

Grundrelation

Für involutorische Gruppenelemente ${\displaystyle \alpha ,\beta }$ wird eine namenlose Relation definiert, es zeigt sich, dass diese Relation sowohl Inzidenz als auch Senkrechtstehen und noch einige andere Beziehungen beschreibt: Seien ${\displaystyle \alpha ,\beta }$ involutorische Gruppenelemente, dann gilt ${\displaystyle \alpha |\beta }$ genau dann, wenn eine der folgenden äquivalenten Bedingungen erfüllt ist:

• ${\displaystyle \alpha \beta }$ ist involutorisch,
• ${\displaystyle \alpha \beta =\beta \alpha }$ und ${\displaystyle \alpha \neq \beta }$,
• ${\displaystyle \alpha ^{\beta }=\alpha }$ und ${\displaystyle \alpha \neq \beta }$ (geometrische Interpretation: Die Bewegung ${\displaystyle \beta }$ bildet das „geometrische Objekt“ ${\displaystyle \alpha }$ z. B. Punkt oder Gerade auf sich selbst ab),
• ${\displaystyle \beta ^{\alpha }=\beta }$ und ${\displaystyle \alpha \neq \beta }$.

Die Grundrelation ist symmetrisch und irreflexiv.

Abkürzungen

Statt „${\displaystyle \alpha _{1}|\beta }$ und ${\displaystyle \alpha _{2}|\beta }$“ wird abkürzend ${\displaystyle \alpha _{1},\alpha _{2}|\beta }$ geschrieben ${\displaystyle \alpha _{1},\alpha _{2}|\beta _{1},\beta _{2}}$ bedeutet: Jedes linksstehende Element ${\displaystyle \alpha _{k}}$ steht mit jedem rechtsstehenden ${\displaystyle \beta _{j}}$ in Relation usw.

Gruppentheoretische Formulierung der Axiome

Axiom D (Axiom vom Dreiseit): Es gibt zwei senkrechte Geraden ${\displaystyle g}$, ${\displaystyle h}$ und eine Gerade ${\displaystyle j}$, die weder zu ${\displaystyle g}$ noch zu ${\displaystyle h}$ senkrecht ist und nicht mit dem Punkt ${\displaystyle gh}$ inzidiert.

Grundannahme: Es sei ein aus involutorischen Elementen bestehendes, invariantes Erzeugendensystem ${\displaystyle {\mathfrak {S}}}$ einer Gruppe ${\displaystyle {\mathfrak {G}}}$ gegeben.

Die Elemente von ${\displaystyle {\mathfrak {S}}}$ werden mit kleinen lateinischen Buchstaben bezeichnet (sie spielen die Rolle der Geraden und Achsenspiegelungen), die involutorischen Elemente der Gruppe ${\displaystyle {\mathfrak {G}}}$, welche als Produkt von zwei Elementen des Erzeugendensystems ${\displaystyle {\mathfrak {S}}}$ darstellbar sind – also die in der Form ${\displaystyle ab}$ mit ${\displaystyle a|b}$ darstellbaren Elemente der Gruppe – werden mit großen lateinischen Buchstaben bezeichnet (sie spielen die Rolle der Punkte und Punktspiegelungen).

Axiom 1: Zu ${\displaystyle P,Q}$ gibt es stets ein ${\displaystyle g}$ mit ${\displaystyle P,Q|g}$ (Existenz der Verbindungsgeraden).

Axiom 2: Aus ${\displaystyle P,Q|g,h}$ folgt ${\displaystyle P=Q}$ oder ${\displaystyle g=h}$ (Eindeutigkeit der Verbindungsgeraden, zwei Geraden haben höchstens einen Schnittpunkt).

Axiom 3: Gilt ${\displaystyle a,b,c|P}$, so gibt es ein ${\displaystyle d}$, so dass ${\displaystyle abc=d}$ ist (Satz von den drei Spiegelungen für drei kopunktale Geraden).

Axiom 4: Gilt ${\displaystyle a,b,c|g}$, so gibt es ein ${\displaystyle d}$, so dass ${\displaystyle abc=d}$ ist (Satz von den drei Spiegelungen für drei lotgleiche Geraden).

Axiom D: Es gibt ${\displaystyle g,h,j}$ derart, dass ${\displaystyle g|h}$ und weder ${\displaystyle j|g}$ noch ${\displaystyle j|h}$ noch ${\displaystyle j|gh}$ gilt (Axiom vom Dreiseit).

Vergleiche zur geometrischen Bedeutung der Axiome die Abbildung rechts für das Axiom D, zu den Axiomen 3 und 4 siehe weiter unten

Weitere Begriffe und Relationen

Punkte, Geraden, Inzidenz- und Senkrechtrelation

• Die Elemente des Erzeugendensystems ${\displaystyle {\mathfrak {S}}}$ werden als Geraden interpretiert.
• Die involutorischen Elemente ${\displaystyle P\in {\mathfrak {G}}}$, für die eine Darstellung ${\displaystyle P=ab,\;a,b\in {\mathfrak {S}}}$ existiert, werden als Punkte interpretiert.
• Ist für einen Punkt ${\displaystyle P}$ und eine Gerade ${\displaystyle g}$ das Produkt ${\displaystyle Pg}$ (oder gleichwertig ${\displaystyle gP}$) involutorisch, dann sagt man: „${\displaystyle P}$ und ${\displaystyle g}$ inzidieren“, kurz:${\displaystyle PIg:\Leftrightarrow P|g}$.
• Ist für zwei Geraden ${\displaystyle a,b}$ das Produkt ${\displaystyle ab}$ involutorisch, dann sagt man „${\displaystyle a}$ ist senkrecht zu ${\displaystyle b}$“, kurz ${\displaystyle a\perp b:\Leftrightarrow a|b}$.

Zwei senkrechte Geraden bestimmen also einen Punkt, senkrechte Geraden schneiden sich immer, ein Punkt kommutiert mit jeder Geraden, die mit ihm inzidiert. Zwei Geraden kommutieren genau dann, wenn sie zueinander senkrecht stehen.

${\displaystyle ({\mathfrak {G}},{\mathfrak {S}})}$ heißt, wenn die Grundannahme und die Axiome erfüllt sind, erzeugte Bewegungsgruppe. Die geometrische Struktur ${\displaystyle ({\mathfrak {P}},{\mathfrak {S}},I,\perp )}$, die sich aus der Bewegungsgruppe durch die geometrischen Interpretationen ergibt, heißt die Gruppenebene von ${\displaystyle ({\mathfrak {G}},{\mathfrak {S}})}$.

Transformieren

Ist ${\displaystyle \alpha \in {\mathfrak {G}}}$ ein beliebiges Gruppenelement, dann gilt nach Definition der Punkte und Geraden, insbesondere aufgrund der Invarianz von ${\displaystyle {\mathfrak {S}}}$ unter Konjugation:

• für jeden Punkt ${\displaystyle P}$ ist das transformierte Objekt ${\displaystyle P^{\alpha }}$ ein Punkt,
• für jede Gerade ${\displaystyle g}$ ist das transformierte Objekt ${\displaystyle g^{\alpha }}$ eine Gerade,
• die Inzidenzrelation und die Senkrechtrelation bleiben bei Transformationen erhalten.

Durch das „Transformieren“, also das gruppentheoretische Konjugieren, operiert die Gruppe auf sich selbst und insbesondere auf den Elementen, die geometrisch als Geraden und Punkte interpretiert werden. Als Transformationsgruppe der Punkte und Geraden wird ${\displaystyle {\mathfrak {G}}}$ als Gruppe der Bewegungen der Gruppenebene aus Punkten und Geraden bezeichnet.

Zunächst ist nach Konstruktion klar, dass durch die Transformation ein Epimorphismus der Gruppe ${\displaystyle {\mathfrak {G}}}$ auf die Gruppe ihrer inneren Automorphismen gegeben ist. Tatsächlich gilt:

• Das Zentrum von ${\displaystyle {\mathfrak {G}}}$ besteht nur aus dem Einselement.^[6] Und daher:
• Die axiomatisch beschriebene Bewegungsgruppe ${\displaystyle {\mathfrak {G}}}$ ist isomorph zur Gruppe der Bewegungen ihrer Gruppenebene.^[7]

Verbindbarkeit

Besteht für drei involutorische Elemente ${\displaystyle \rho _{1},\rho _{2},\sigma }$ die Relation ${\displaystyle \rho _{1},\rho _{2}|\sigma }$, dann heißt ${\displaystyle \sigma }$ eine Verbindung von ${\displaystyle \rho _{1},\rho _{2}}$. Wichtige konkrete geometrische Interpretationen der Verbindbarkeit:

• ${\displaystyle A,B|g}$: Die Punkte ${\displaystyle A,B}$ sind durch die Gerade ${\displaystyle g}$ verbunden. – Die Existenz dieser Verbindungsgeraden ist durch das Axiom 1, ihre Eindeutigkeit im Fall ${\displaystyle A\neq B}$ durch Axiom 2 gesichert.
• ${\displaystyle g,h|A}$: Die beiden Geraden sind kopunktal. Existiert für zwei verschiedene Geraden ein Verbindungspunkt, dann gibt es nach Axiom 2 keinen weiteren.
• ${\displaystyle g,h|l}$: Die Geraden ${\displaystyle g,h}$ besitzen ein gemeinsames Lot ${\displaystyle l}$. Sie heißen dann auch lotgleich. Die geometrische Aussage: „Jede Gerade besitzt ein Lot“ folgt aus der Tatsache, dass jede Gerade einen Punkt enthält (aus den gruppentheoretischen Axiomen nicht ganz trivial zu beweisen) und dann einfach aus der Definition eines Punktes als Produkt zweier senkrechter Geraden.

Die Lotgleichheit zweier Geraden ist in der absoluten Geometrie eine Äquivalenzrelation, die die Parallelität im Sinne der Inzidenz oft ersetzen kann.

Büschel

Von Geraden ${\displaystyle a,b,c\in {\mathfrak {S}}}$ sagt man „sie liegen im Büschel“, wenn ${\displaystyle abc\in {\mathfrak {S}}}$ also eine Gerade ist. Die dreistellige Relation Im-Büschel-Liegen ${\displaystyle B(a,b,c)}$ hat offensichtlich die folgenden Eigenschaften:

• (dreistellige) Reflexivität: Stimmen mindestens zwei der Garaden ${\displaystyle a,b,c}$ überein, dann gilt ${\displaystyle B(a,b,c)}$. Zum Beispiel ${\displaystyle B(a,a,c):aac=c}$, da ${\displaystyle a}$ Involution ist, ${\displaystyle B(a,b,a):aba=b^{a}\;}$ ist eine Gerade, weil ${\displaystyle {\mathfrak {S}}}$ invariant ist.
• (dreistellige) Symmetrie: Gilt ${\displaystyle B(a,b,c)}$, so trifft die Relation auch für jede Permutation der Geraden zu. Zum Beispiel ${\displaystyle abc\in {\mathfrak {S}}\Rightarrow bca=aa\cdot bca=a(abc)a=(abc)^{a}}$; ${\displaystyle \;abc\in {\mathfrak {S}}\Rightarrow abc=(abc)^{-1}=cba}$ usw.

Nicht so offensichtlich ist die:

• (dreistellige) Transitivität: Gilt ${\displaystyle B(a,b,c),B(a,b,d)}$ und ${\displaystyle a\neq b}$, dann folgt ${\displaystyle B(a,c,d)}$.^[8]

Die Büschelrelation erzeugt als dreistellige „Äquivalenzrelation“ eine Aufteilung der Geradenmenge in Geradenbüschel mit folgenden Eigenschaften, die den Äquivalenzklasseneigenschaften einer zweistelligen Äquivalenzrelation ähneln (und rein mengentheoretische Folgerungen aus den genannten Relationeneigenschaften, der dreistelligen Reflexivität, Symmetrie und Transitivität sind):

• Für drei verschiedene Geraden in einem Büschel gilt die Relation.
• Gilt die Relation für zwei verschiedene Geraden eines Büschels und eine dritte Gerade, dann liegt auch diese im Büschel.
• Zwei verschiedene Geraden eines Büschels bestimmen dieses eindeutig.
• Zwei verschiedene Büschel haben höchstens ein Element gemein.

Geometrisch treten in der absoluten Geometrie drei Arten von Geradenbüscheln auf:

1. Büschel kopunktaler Geraden (die klassischen Büschel, wie sie im projektiven Raum auftreten),
2. Büschel lotgleicher Geraden, Lotbüschel,
3. „freie“ Büschel (weder Punkt- noch Lotbüschel).

Für die ersten zwei Arten gilt ein „Alles oder Nichts“-Prinzip: Ist ein Punktbüschel zugleich Lotbüschel, dann sind es alle! Dies ist genau dann der Fall, wenn die Geometrie elliptisch ist, in diesem Fall existieren auch keine freien Büschel. In jeder nichtelliptischen Geometrie schließen sich die drei Fälle aus. Alle drei Arten werden bei der Einbettung der absoluten Geometrie in eine projektive Idealebene zu Idealpunkten. Genau diese Idealpunkte sind dann die Punkte der Idealebene.

Spiegelbildliche Lage, Winkel, Drehungen

Die in Axiom 3 geforderte vierte Spiegelachse ${\displaystyle d}$ zu drei kopunktalen Geraden ${\displaystyle a,b,c}$. Es gilt dann ${\displaystyle ab=dc}$. Die Paare ${\displaystyle (a,b),(d,c)}$ ergeben bei Hintereinanderausführung die gleiche Transformation, eine Drehung um ${\displaystyle o}$. Sie repräsentieren also den gleichen „Drehwinkel“.

Sind die Geraden ${\displaystyle a,b,c}$ lotgleich, in der Abbildung alle senkrecht zu ${\displaystyle g}$, dann ist die in Axiom 4 geforderte 4. Spiegelungsachse ${\displaystyle d}$ ebenfalls senkrecht zu ${\displaystyle g}$.

Gilt für 4 Geraden ${\displaystyle a,b,c,d\;ab=dc}$, dann sagt man nach Hjelmslev:^[9] „Die Geraden ${\displaystyle b,d}$ liegen zueinander spiegelbildlich in Bezug auf die Geraden ${\displaystyle a,c}$.“ Dann liegen auch die Geraden ${\displaystyle a,c}$ spiegelbildlich zueinander in Bezug auf ${\displaystyle b,d}$, vergleiche die Abbildungen. Ist dabei ${\displaystyle a=c}$, also ${\displaystyle ab=da}$ und gleichwertig ${\displaystyle b^{a}=d}$, dann sagt man: „Die Geraden ${\displaystyle b,d}$ liegen spiegelbildlich zueinander in Bezug auf die Achse ${\displaystyle a}$“. Aus den Axiomen folgt nicht, dass es zu zwei gegebenen verschiedenen Geraden ${\displaystyle b,d}$ eine solche Mittellinie gibt.

Für Paare ${\displaystyle (a,b),(d,c)}$ von Geraden in einem Punktbüschel ist durch die symmetrische Lage eine Äquivalenzrelation gegeben: ${\displaystyle (a,b)\sim (d,c):\Leftrightarrow ab=dc}$. Zwei Paare, die zueinander in der ${\displaystyle \sim }$-Relation stehen, bestimmen die gleiche „Drehung“ um den Punkt, mit dem sie gemeinsam inzidieren. Daher kann man die Äquivalenzklassen als Winkel auffassen. Der in der Abbildung rechts (kopunktale Geraden) eingezeichnete (euklidische) Winkel zwischen zwei Achsen ist der halbe euklidische Drehwinkel der Drehung um ${\displaystyle O}$, die durch das Transformieren mit ${\displaystyle ab=dc}$ gegeben ist. In der zweiten Abbildung (lotgleiche Geraden) ist die eingezeichnete (euklidische) Verschiebung die Hälfte der Translation, die durch das Transformieren mit ${\displaystyle ab}$ (links) bzw. ${\displaystyle cd}$ (rechts) im metrisch-euklidischen Fall gegeben ist.

Unterscheidende Axiome

Das Unverbindbarkeitsaxiom${\displaystyle \neg \mathbf {V} }$ in einer metrisch-euklidischen Ebene: Die Geraden ${\displaystyle a}$ und ${\displaystyle b}$ haben ein gemeinsames Lot ${\displaystyle l}$, sind also lotverbunden. Die Gerade ${\displaystyle c}$ (grün) schneidet ${\displaystyle b}$ in ${\displaystyle S}$, ist also mit ${\displaystyle b}$ punktverbunden und kann daher weder mit ${\displaystyle a}$ noch mit ${\displaystyle b}$ durch ein Lot verbunden sein (da ${\displaystyle \mathbf {R} }$ vorausgesetzt wird). Wenn es keinen Schnittpunkt von ${\displaystyle c}$ und ${\displaystyle a}$ gibt, angedeutet durch das rote Fragezeichen, dann gilt in dieser metrisch-euklidischen Ebene das Axiom ${\displaystyle \neg \mathbf {V} }$. Aus der Existenz des fraglichen Punktes folgt nicht das Axiom ${\displaystyle \mathbf {V} }$!

An den folgenden Axiomen gabeln sich die verschiedenen Arten von absoluten Geometrien:

• Verbindbarkeitsaxiom, es spielt die Rolle eines Vollständigkeitsaxioms.
• Existenz eines Polardreiseits (charakterisiert die elliptische Geometrie)
• Existenz eines Rechtsseits (charakterisiert im Wesentlichen die euklidische Geometrie, zusammen mit dem Verbindbarkeitsaxiom genau diese).
• Axiom ${\displaystyle \mathbf {H} }$ schränkt die Möglichkeiten der Unverbindbarkeit ein. Es charakterisiert zusammen mit der Negation des Verbindbarkeitsaxioms die hyperbolische Geometrie.

Polardreiseit und elliptische Ebenen

Ein Polardreiseit ist charakteristisch für die elliptische Geometrie. Alle rot gekennzeichneten Winkel sind Rechte. Der Punkt ${\displaystyle C}$ ist Pol der Geraden ${\displaystyle c}$, diese ist die Polare von ${\displaystyle C}$. Alle Geraden durch ${\displaystyle C}$ schneiden ${\displaystyle c}$ und sind Lote auf ${\displaystyle c}$. Jede zu ${\displaystyle c}$ senkrechte Gerade geht durch den Punkt ${\displaystyle C}$.

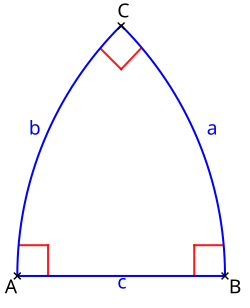
Geometrisch ist ein Polardreiseit ein Dreiseit (drei Geraden, die nicht kopunktal sind), bei dem jede Gerade auf beiden anderen senkrecht steht. In der Sprache der Gruppenebene sind das drei verschiedene ${\displaystyle a,b,c\in {\mathfrak {S}}}$, bei denen je zwei verschiedene zueinander in der ${\displaystyle |}$ Relation stehen, das heißt bei den unterschiedlichen äquivalenten Aussagen und Interpretationen:

Jedes Produkt von zwei dieser Elemente

• ist eine Involution, d. h. ein Punkt,
• ist dem umgekehrten Produkt gleich.

• Aus der zweiten Aussage folgt, dass die drei Elemente kommutieren.

Nennt man z. B. das Produkt ${\displaystyle ab=:C}$ Punkt ${\displaystyle C}$, dann sind ${\displaystyle aC=aab=b,Cb=abb=a}$ involutorisch, also liegt ${\displaystyle C}$ auf ${\displaystyle a}$ und ${\displaystyle b}$, ist also der eindeutig bestimmte Schnittpunkt dieser senkrechten Geraden. Analog sind ${\displaystyle B:=ac}$, ${\displaystyle A:=bc}$ die anderen beiden Ecken des Dreiseits. Da die drei Geraden kommutieren, ist ${\displaystyle (Cc)^{2}=(abc)^{2}=a^{2}b^{2}c^{2}=1}$. ${\displaystyle Cc}$ kann aber nicht involutorisch sein, sonst wäre ${\displaystyle C}$ auch in der Geraden ${\displaystyle c}$ enthalten, was der Eindeutigkeit des Lotes in einem Punkt der Geraden ${\displaystyle c}$ widerspräche. Also gilt ${\displaystyle abc=1}$ und das Entsprechende für jede Permutation der drei Geraden im Produkt.

Gilt umgekehrt ${\displaystyle abc=1}$ für drei Geraden, so müssen sie paarweise verschieden sein (sonst wäre das Produkt entweder eine Gerade oder eine transformierte Gerade also wieder eine Gerade und jedenfalls eine Involution). Es folgt ${\displaystyle ab=c,a=cb,b=ac}$ und wieder hat man drei verschiedene paarweise senkrechte Geraden, die zugleich als Produkte von Geraden Punkte sind.

Axiom ${\displaystyle \neg \mathbf {P} }$ (Es existiert kein Polardreiseit) Es ist stets ${\displaystyle abc\neq 1}$.

Axiom ${\displaystyle \mathbf {P} }$ (Es existiert ein Polardreiseit) Es gibt ${\displaystyle a,b,c}$ mit ${\displaystyle abc=1}$.

Aus dem Axiom ${\displaystyle \neg \mathbf {P} }$ folgt mit den gemeinsamen Axiomen: Kein Produkt einer ungeraden Anzahl von Erzeugenden ist einem Produkt einer geraden Anzahl von Erzeugenden gleich. In diesem Fall ist die Untergruppe ${\displaystyle {\mathfrak {U}}<{\mathfrak {G}}}$ der durch eine gerade Anzahl von Erzeugenden darstellbaren Gruppenelemente eine Untergruppe vom Index 2 in ${\displaystyle {\mathfrak {G}}}$. Dann gilt:

• Es ist ${\displaystyle {\mathfrak {U}}=\{ab:a,b\in {\mathfrak {S}}\}}$,
• Jeder Punkt gehört zu der Untergruppe ${\displaystyle {\mathfrak {U}}}$,
• jedes Element der (echten) Nebenklasse von ${\displaystyle {\mathfrak {U}}}$, der Klasse der durch eine ungerade Zahl von erzeugenden Achsenspiegelungen darstellbaren Gruppenelemente, ist in der Form ${\displaystyle aB}$, als Gleitspiegelung darstellbar,
• kein Produkt von zwei Punkten ist involutorisch,
• kein Punkt ist einer Geraden gleich,
• die involutorischen Elemente von ${\displaystyle {\mathfrak {U}}}$ sind genau die Punkte,
• die involutorischen Elemente der Nebenklasse sind genau die Geraden.

Aus dem Axiom ${\displaystyle \mathbf {P} }$ folgt mit den gemeinsamen Axiomen: Jedes Produkt einer geraden Anzahl von Erzeugenden ist einem Produkt einer ungeraden Anzahl von Erzeugenden gleich, es ist ${\displaystyle {\mathfrak {U}}={\mathfrak {G}}}$, und außerdem gilt:

• Jedes Gruppenelement ist in der Form ${\displaystyle ab}$ darstellbar,
• also ist jede Gerade ${\displaystyle c}$ einem Punkt ${\displaystyle C}$ gleich, man nennt ihn den Pol der Geraden, die Gerade Polare ihres Pols^[10]
• ${\displaystyle c=ab}$ bedeutet zugleich ${\displaystyle abc=1}$, also gehört jeder Punkt als Ecke zu einem Polardreieck, jede Gerade als Seite zu einem Polardreiseit.

Rechtseit und metrisch-euklidische Ebenen

Ein Rechtseit, die rot gekennzeichneten Winkel sind Rechte. Die Existenz eines Rechtseits charakterisiert die metrisch-euklidischen Ebenen unter den ebenen Modellen der absoluten Geometrie.

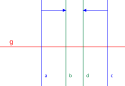
• Axiom ${\displaystyle \mathbf {R} }$: Es gibt ${\displaystyle a,b,c,d}$ mit ${\displaystyle a,c\perp b,d}$ und ${\displaystyle a\neq c,b\neq d}$, das heißt, es gibt ein Rechtseit, vgl. die Abbildung rechts.
• Axiom ${\displaystyle \neg \mathbf {R} }$: Aus ${\displaystyle a,c\perp b,d}$ folgt ${\displaystyle a=c}$ oder ${\displaystyle b=d}$.

Geometrien, für die ${\displaystyle \mathbf {R} }$ gilt, werden metrisch-euklidisch genannt. In einer metrisch-euklidischen Ebene wird die Lotgleichheit als Parallelität definiert: ${\displaystyle a\|_{R}b}$ soll gelten, wenn die beiden Geraden ein gemeinsames Lot haben. Lotgleiche Geraden haben keinen oder alle Punkte gemein, sind also Nichtschneidende oder identisch. Zwei Geraden, die einander nicht schneiden, müssen aber nicht unbedingt ein gemeinsames Lot besitzen (siehe bei den Modellen). Das Verbindbarkeitsaxiom ${\displaystyle \mathbf {V} ^{*}}$ schließt die Existenz solcher Nichtschneidender, die nicht lotgleich sind, aus.

Aus dem Axiom ${\displaystyle \mathbf {P} }$ folgt das Axiom ${\displaystyle \neg \mathbf {R} }$, gleichwertig: Aus dem Axiom ${\displaystyle \mathbf {R} }$ folgt das Axiom ${\displaystyle \neg \mathbf {P} }$ (immer auf der Grundlage der gemeinsamen Axiome). Ein Polardreiseit kann nicht zugleich mit einem Rechtsseit existieren. Etwas formeller: Keine metrisch-euklidische Geometrie ist elliptisch, keine elliptische metrisch-euklidisch.

Aus dem Axiom ${\displaystyle \mathbf {R} }$ folgt der Rechtsseitsatz:^[11] Aus ${\displaystyle a,b\perp c}$ und ${\displaystyle a\perp d}$ folgt ${\displaystyle b\perp d}$. ${\displaystyle (\mathbf {R} )}$ Vergleiche die Abbildung.

Trotz einer gewissen Ähnlichkeit zu Axiom ${\displaystyle \mathbf {R} }$ ist der Rechtseitsatz ein Schließungssatz mit Orthogonalität – aus drei Senkrechtrelationen in einem Vierseit folgt die Vierte – während das Axiom eine reine Existenzaussage ist.

Verbindbarkeitsaxiom und Axiom H: Hyperbolische Ebenen

Verbindbarkeit im Kleinschen Kreisscheibenmodell: Zwei hyperbolische Geraden (grün) deren projektive Trägergeraden sich im Äußeren des Kreises (im Idealpunkt ${\displaystyle P}$) treffen, haben den eigentlichen Teil der Polaren ${\displaystyle l}$ von ${\displaystyle P}$ (rot), der wieder im Inneren des Kreises liegt, als einziges gemeinsames Lot. Geraden, die sich im Kreisinneren treffen, sind punktverbunden. Zwei verschiedene Geraden können nur punkt- oder lotverbindbar sein, nie beides (Axiom${\displaystyle \neg \mathbf {P} }$ vorausgesetzt).

Hier wird „Verbindbarkeit“ in einem etwas engeren Sinn als weiter oben verstanden. Die Axiome können auch äquivalent allgemeiner formuliert werden, aber sie sollten hier als Axiome formal wenig voraussetzen. Die hier gegebene Formulierung ist die von Bachmann zur Beschreibung der hyperbolischen Geometrie gegebene:^[12]

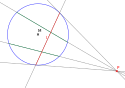
• Axiom ${\displaystyle \mathbf {V} ^{*}}$ (Verbindbarkeitsaxiom) Zu zwei Geraden ${\displaystyle a,b}$ gibt es stets einen Punkt ${\displaystyle C}$ mit ${\displaystyle a,b|C}$ oder eine Gerade ${\displaystyle g}$ mit ${\displaystyle a,b|g}$. Geometrisch formuliert: Zwei Geraden haben entweder einen Punkt oder ein Lot gemeinsam.

Gibt es für zwei Geraden einen solchen Schnittpunkt oder ein gemeinsames Lot, dann nennt man sie verbindbar (im engeren Sinn).

• Axiom ${\displaystyle \neg \mathbf {V} ^{*}}$: Es gibt ${\displaystyle a,b}$, die unverbindbar sind.
• Axiom ${\displaystyle \mathbf {H} }$: Gilt ${\displaystyle a,b,c|P}$ und sind ${\displaystyle a,g}$ und ${\displaystyle b,g}$ und ${\displaystyle c,g}$ jeweils unverbindbar, so gilt ${\displaystyle a=b}$ oder ${\displaystyle a=c}$ oder ${\displaystyle b=c}$.

Anders formuliert besagt Axiom ${\displaystyle \mathbf {H} }$: In einem Büschel kopunktaler Geraden gibt es höchstens zwei verschiedene, die mit einer gegebenen Geraden ${\displaystyle g}$ unverbindbar sind (weder einen Punkt noch ein Lot mit ihr gemeinsam haben).

Das Axiom${\displaystyle \mathbf {H} }$ der hyperbolischen Geometrie im Kleinschen Kreisscheibenmodell: Das Punktbüschel durch P enthält genau zwei Geraden, die g in einem „Ende“, also auf dem Randkreis treffen. Nur diese beiden Geraden des Punktbüschels sind mit g unverbindbar. Man beachte, das die Enden von ${\displaystyle g}$ uneigentliche Idealpunkte der hyperbolischen Ebene sind. Zum Axiom ${\displaystyle D^{*}}$: Die Lote durch den Kreismittelpunkt ${\displaystyle M}$ sind im Kreisscheibenmodell euklidische Lote auf die Kreissehnen. Denkt man sich von ${\displaystyle M}$ auf ${\displaystyle g}$ diese Lotgerade ${\displaystyle h}$ gezeichnet, dann erfüllen ${\displaystyle g}$ und ${\displaystyle h}$ zusammen mit jeder der eingezeichneten Geraden durch ${\displaystyle P}$ als mit ${\displaystyle g}$ unverbindbare Gerade ${\displaystyle j}$ das Axiom.

Eine Geometrie, die ${\displaystyle \neg \mathbf {V} ^{*}}$ und ${\displaystyle \mathbf {H} }$ erfüllt, wird als hyperbolische Geometrie bezeichnet.

Man kann das um die Unvollvollständigkeitsaxiome ${\displaystyle \neg \mathbf {V} ^{*}}$ und ${\displaystyle \mathbf {H} }$ als Zusatzaxiome erweiterte Axiomensystem der hyperbolischen Geometrie äquivalent, aber ein wenig kürzer beschreiben, indem man ${\displaystyle \neg \mathbf {V} ^{*}}$ mit dem gemeinsamen Axiom ${\displaystyle D}$ zusammenfasst zum Axiom

${\displaystyle D^{*}}$: Es gibt ${\displaystyle g,h,j}$, mit ${\displaystyle g\perp h}$ und ${\displaystyle g,j}$ unverbindbar (im oben beschriebenen engeren Sinn: ${\displaystyle g,j}$ haben weder einen Punkt noch ein Lot gemein).^[12]

Man kann also die hyperbolischen Bewegungsgruppen auch gleichwertig durch das Axiomensystem beschreiben, das man erhält, wenn man zusätzlich das Axiom ${\displaystyle \mathbf {H} }$ fordert und die Axiome ${\displaystyle \neg \mathbf {V} ^{*}}$ und ${\displaystyle D}$ durch ${\displaystyle D^{*}}$ ersetzt.^[12]

Weiterhin gilt:^[12]

• Aus ${\displaystyle \mathbf {P} }$ folgt das Axiom ${\displaystyle \mathbf {V} ^{*}}$, („jede elliptische Geometrie ist vollständig“),
• aus ${\displaystyle \neg \mathbf {V} ^{*}}$ und ${\displaystyle \mathbf {R} }$ folgt die Ungültigkeit von ${\displaystyle \mathbf {H} }$ („keine unvollständige metrisch-euklidische Ebene ist hyperbolisch“),
• Jede hyperbolische Geometrie ist wegen ${\displaystyle \neg \mathbf {V} ^{*}}$ „unvollständig“.

Daher kann eine Gruppenebene nur höchstens einer der Klassen „elliptische“, „metrisch-euklidische“ oder „hyperbolische“ Geometrie angehören.

Halbelliptische Ebenen

Eine Gruppenebene, die die Axiome ${\displaystyle \neg \mathbf {R} }$, ${\displaystyle \mathbf {V} ^{*}}$ und ${\displaystyle \neg \mathbf {P} }$ erfüllt, wird als halbelliptisch bezeichnet, sie lässt sich auch gleichwertig durch das Axiom

„Zwei verschiedene Geraden haben entweder genau ein Lot oder genau einen Punkt gemeinsam, nie beides.“^[13]

beschreiben. Bei der Einbettung in einen projektiv-metrischen Raum werden halbelliptische Gruppen zu elliptischen Gruppen vervollständigt; ihre Bewegungsgruppe erweist sich dabei als volle elliptische Gruppe ${\displaystyle {\mathfrak {G}}}$, aber das axiomatisch beschriebene Erzeugendensystem ${\displaystyle {\mathfrak {S}}}$, das heißt geometrisch die Geraden der Ebene bilden eine echte Teilmenge ${\displaystyle {\mathfrak {S}}\subsetneq {\mathfrak {S}}'}$ der projektiven Geradenmenge und hier gruppentheoretisch der Menge aller involutorischer Gruppenelemente ${\displaystyle {\mathfrak {S}}'}$.

Einbettung in die projektiv-metrische Idealebene

Abgesehen von der Äquivalenz des geometrisch formulierten Axiomensystems zu dem gruppentheoretisch formulierten, ist zunächst nicht klar, in welchem Sinn es sich bei den axiomatisch beschriebenen Gruppen mit Erzeugendensystem aus involutorischen Elementen um „geometrische Abbildungsgruppen“ handelt. Die Einbettung in eine projektiv-metrische Ebene (die Idealebene der Gruppenebene) macht dies deutlich und leistet dabei viererlei:^[14]

1. Für die Inzidenzrelation: Die Menge der Achsenspiegelungen ${\displaystyle {\mathfrak {S}}}$ wird injektiv auf eine Teilmenge der Idealgeradenmenge (die eigentlichen Idealgeraden) abgebildet und die Menge der Geradenbüschel bijektiv auf die Punktmenge der projektiven Idealebene. Dabei bleibt die Inzidenzrelation für eigentliche Punkte (Punktbüschel der Gruppenebene) und eigentliche Geraden erhalten.
2. Für die Orthogonalität: Die Orthogonalität in der Gruppenebene wird zu einer Idealgerade-Idealpol Beziehung in der projektiven Idealebene fortgesetzt. Zwei Geraden der Gruppenebene (eigentliche Idealgeraden) sind senkrecht zueinander, wenn die eine im Idealpol (einem Büschel) der anderen enthalten ist. Die Fortsetzung auf beliebige Idealgeraden und deren Pole ist eindeutig.
3. Für die Gruppenstruktur: Die axiomatisch beschriebene Bewegungsgruppe ${\displaystyle {\mathfrak {G}}}$ erweist sich als isomorph zu einer wohlbestimmten Untergruppe der orthogonalen Gruppe der projektiv-metrischen Ebene, in die eingebettet wird. Die orthogonale Gruppe ist dabei diejenige Untergruppe der projektiven Gruppe ${\displaystyle \operatorname {PGL} (3,K)}$, die die Polarstruktur invariant lässt. Das Erzeugendensystem ${\displaystyle {\mathfrak {S}}}$ bestimmt diese Untergruppe ${\displaystyle {\mathfrak {G}}}$ eindeutig, aber das Erzeugendensystem ${\displaystyle {\mathfrak {S}}}$ ist durch ${\displaystyle {\mathfrak {G}}}$ im Allgemeinen nicht eindeutig bestimmt.
4. Für die algebraische Darstellung durch Koordinaten: Die Bewegungsgruppe bestimmt einen eindeutigen Koordinatenkörper ${\displaystyle K}$ (den Koordinatenkörper der projektiv-metrischen Ebene) und im Fall einer hyperbolischen Bewegungsgruppe durch ihr Erzeugendensystem ${\displaystyle {\mathfrak {S}}}$ auch eine eindeutige Anordnung dieses Körpers. Zusätzliche Eigenschaften der Bewegungsgruppe (Halbierbarkeit von Rechten Winkeln, geometrische Anordnung, Freie Beweglichkeit, …) entsprechen häufig einer bestimmten Klasse von Körpern.

Dabei beobachtet man zusätzlich und nebenher, dass die Halbspiegelungen, mit denen potentielle Idealgeraden (technisch) auf eigentliche Idealgeraden „kontrahiert“ werden, injektive Abbildungen auf der Menge der eigentlichen Idealgeraden darstellen, die nur dann surjektiv sind, wenn die Geometrie entweder elliptisch oder euklidisch ist. Daraus folgt, dass nur in diesen beiden Hauptfällen die metrische Ebene endlich sein könnte. – Tatsächlich existieren nur für den euklidischen Fall endliche Modelle. Im elliptischen Fall existieren die erforderlichen projektiven, elliptischen Polaritäten nur über unendlichen Körpern, siehe dazu Korrelation (Projektive Geometrie)#Polaritäten über endlichen Räumen.

Beziehungen zwischen Gruppenebene und Idealebene

• Jedes Geradenbüschel der Gruppenebene von ${\displaystyle ({\mathfrak {G}},{\mathfrak {S}})}$ ist ein Idealpunkt. Die Punktbüschel der Gruppenebene sind die eigentlichen Idealpunkte. Dies zeigt, dass die Idealebene minimal hinsichtlich der Punktmenge ist.
• Jeder eigentliche Idealpunkt (also jedes Punktbüschel) inzidiert auch in der Idealebene ausschließlich mit eigentlichen Idealgeraden. „In einem beliebigen Punkt stimmen absolute Geometrie und projektive Geometrie überein.“ Man nennt die Gruppenebene wegen dieser Eigenschaft auch eine lokal vollständige Teilebene ihrer Idealebene.
• Jede Bewegung ${\displaystyle \gamma \in {\mathfrak {G}}}$ bestimmt in der Idealebene eine eindeutige Projektivität, die die Gesamtheit der eigentlichen Idealpunkte und -geraden inzidenztreu durch Transformieren je auf sich abbildet.
• Die Spiegelung in der Gruppenebene an einer Geraden ${\displaystyle c}$, das heißt das Transformieren mit ${\displaystyle c\in {\mathfrak {S}}}$ induziert in der Idealebene die^[15] involutorische Perspektivität mit der eigentlichen Idealgeraden ${\displaystyle g(c)}$ als Achse und deren Pol ${\displaystyle G(c)}$ als Zentrum.^[16]

• Jede Idealgerade ist bestimmt als Fixpunktmenge (von fixierten Idealpunkten) einer involutorischen, polaritätstreuen Perspektivität ${\displaystyle \pi _{Z}}$, mit einem Idealpunkt ${\displaystyle Z}$, dem sie nicht angehört, als Zentrum – der Punkt ${\displaystyle Z}$ selbst ist der einzige Fixpunkt von ${\displaystyle \pi _{Z}}$, der nicht zu der Idealgeraden gehören soll. Im metrisch-euklidischen Sonderfall ist zusätzlich noch die „Ferngerade“ eine uneigentliche Idealgerade, an ihr kann nicht gespiegelt werden.^[17] Sie ist die Menge der (idealen) Pole aller eigentlichen Idealgeraden, mit anderen Worten: Die Menge aller Lotbüschel.

Mehrdimensionale Verallgemeinerung

Die gruppentheoretisch formulierten Axiome für eine absolute Geometrie lassen sich auf Räume der Dimension ${\displaystyle n>2}$ verallgemeinern:^[18] Grundannahme: Sei ${\displaystyle ({\mathfrak {G}},{\mathfrak {S}})}$ eine erzeugte Gruppe, ${\displaystyle {\mathfrak {S}}}$ invariantes Erzeugendensystem aus involutorischen Elementen. Die Grundrelation ${\displaystyle |}$ für involutorische Gruppenelemente wird wie im zweidimensionalen Fall definiert. Es wird vereinbart, dass Ausdrücke wie ${\displaystyle \alpha _{1},\alpha _{2}|\alpha _{3},\alpha _{4}|\alpha _{5}}$ als Abkürzung für Konjunktionen stehen: Steht zwischen zwei Elementen ${\displaystyle \alpha _{j},\alpha _{k}}$ mindestens ein ${\displaystyle |}$-Symbol, dann soll zwischen ihnen die Relation bestehen. Im Beispiel ist etwa ${\displaystyle \alpha _{1}|\alpha _{5}}$ ausgesagt, über die Beziehung zwischen ${\displaystyle \alpha _{3}}$ und ${\displaystyle \alpha _{4}}$ dagegen nichts.

Jedes Element von ${\displaystyle {\mathfrak {S}}}$ wird interpretiert als Spiegelung an einer Hyperebene und mit einem Kleinbuchstaben bezeichnet. ${\displaystyle {\mathfrak {P}}}$ wird definiert als Menge der involutorischen Produkte ${\displaystyle a_{1}\cdot a_{2}\cdots a_{n}}$ mit ${\displaystyle a_{1}|a_{2}|\ldots |a_{n}}$ und interpretiert als Menge der Punktspiegelungen. Die Punktspiegelungen werden mit Großbuchstaben bezeichnet. Gemeinsame Axiome:

Axiom 1_n^*: Zu ${\displaystyle a_{1},\ldots ,a_{n-1},A}$ gibt es ein ${\displaystyle a}$ mit ${\displaystyle a|a_{1},\ldots ,a_{n-1},A}$.

Axiom 1_n: Zu ${\displaystyle a_{1},\ldots ,a_{n-2},A,B}$ mit ${\displaystyle a_{1}|\cdots |a_{n-2}|A,B}$ gibt es ein ${\displaystyle a}$ mit ${\displaystyle a|a_{1},\ldots ,a_{n-2},A,B}$.

Axiom 2_n: Aus ${\displaystyle a_{1}|\cdots |a_{n-2}|a,b|A,B}$ folgt ${\displaystyle a=b}$ oder ${\displaystyle A=B}$.

Axiom 3_n: Aus ${\displaystyle a_{1}|\cdots |a_{n-2},A|a,b,c}$ und ${\displaystyle a_{n-2}\neq A}$ folgt ${\displaystyle abc\in {\mathfrak {S}}}$.

Axiom 4_n: Aus ${\displaystyle a_{1}|\cdots |a_{n-1}|a,b,c}$ folgt ${\displaystyle abc\in {\mathfrak {S}}}$.

Axiom X_n: Es gibt ${\displaystyle a_{1},a_{n}}$ mit ${\displaystyle a_{1}|\cdots |a_{n}}$.

Axiom D_n: Zu ${\displaystyle a_{1},a_{n}}$ mit ${\displaystyle a_{1}|\cdots |a_{n}}$ gibt es ein ${\displaystyle a}$ derart, dass ${\displaystyle a|a_{1},a_{n-1}}$ und weder ${\displaystyle a=a_{n}}$ noch ${\displaystyle a|a_{n}}$ gilt.

Die geometrischen Interpretationen:

• Existenz einer Senkrechten, Axiom 1_n^*: Zu einem Punkt ${\displaystyle A}$ und ${\displaystyle n-1}$ Hyperebenen gibt es eine Hyperebene durch ${\displaystyle A}$, die zu den vorgegebenen senkrecht ist.
• Existenz einer Verbindung, Axiom 1_n: Zu zwei Punkten und ${\displaystyle n-2}$ paarweise senkrechten Hyperebenen, die mit beiden Punkten inzidieren, gibt es eine Hyperebene durch die Punkte, die zu den vorgegebenen Hyperebenen senkrecht ist.
• Eindeutigkeit der Verbindung, Axiom 2_n: Sind die beiden Punkte aus Axiom 1_n verschieden, dann gibt es nur eine solche Hyperebene.
• Existenz der vierten Spiegelungshyperebene, Axiom 3_n: Sind ein Punkt ${\displaystyle A}$ und ${\displaystyle n-2}$ paarweise senkrechte Hyperebenen gegeben, von denen alle bis auf höchstens eine mit ${\displaystyle A}$ inzidieren und auch diese nicht polar zu ${\displaystyle A}$ ist, dann gibt es zu drei Hyperebenen durch ${\displaystyle A}$, die zu den vorgegebenen senkrecht sind, eine vierte Spiegelung(shyperebene).
• Dimension, Axiom X_n: Es gibt ${\displaystyle n}$ paarweise senkrechte Hyperebenen. (Daraus folgt mit der Eindeutigkeit der Verbindung, dass der Raum genau ${\displaystyle n}$-dimensional ist).
• Axiom D_n: Zu ${\displaystyle n}$ paarweise senkrechten Hyperebenen gibt es eine weitere, die zu ${\displaystyle n-1}$ von ihnen senkrecht, aber von der letzten vorgegebenen verschieden und zu ihr nicht senkrecht ist.

Elliptisches Axiom:

Axiom ${\displaystyle \mathbf {P} _{n}}$ (vom Polarsimplex): Es gibt ${\displaystyle a_{1},\ldots ,a_{n+1}}$ mit ${\displaystyle a_{1}|\cdots |a_{n+1}}$.

Modelle der metrischen absoluten Geometrie

Metrisch-euklidische Modelle mit euklidischer Parallelität

• Alle endlichen Modelle der metrischen absoluten Geometrie erfüllen das Parallelenaxiom, sind also affine Räume. Endliche ebene Modelle, die die hier beschriebenen gemeinsamen Axiome 1 bis 4 und D erfüllen, sind genau die endlichen präeuklidischen Ebenen. Die Bewegungsgruppe ${\displaystyle {\mathfrak {G}}}$ einer solchen präeuklidischen Ebene ist die von den senkrechten Achsenspiegelungen ${\displaystyle {\mathfrak {S}}}$ erzeugte Gruppe.
• Jede präeuklidische Ebene liefert ein Modell einer metrischen Ebene. Diese erfüllt dann zusätzlich die Axiome ${\displaystyle \mathbf {R} ,\mathbf {V} ^{*}}$.
• Die präeuklidischen Ebenen lassen sich zu ${\displaystyle n}$-dimensionalen Affinen Räumen mit Orthogonalität erweitern ${\displaystyle (n>2)}$. Diese liefern dann Modelle für metrisch-euklidische Räume mit euklidischer Parallelität.

Hyperbolische Ebenen

• Das Kleinsche Kreisscheiben-Modell der hyperbolischen Geometrie, siehe Hyperbolische Geometrie. Dies ist das bis auf Isomorphie einzige Modell einer reellen hyperbolischen Ebene.

• Allgemein lässt sich über jedem geordneten Körper ${\displaystyle K}$ ein gruppentheoretisches Modell für eine hyperbolische Ebene angeben: Die Bewegungsgruppe ${\displaystyle {\mathfrak {G}}}$ ist ${\displaystyle \operatorname {PGL} (2,K)}$, also die volle Projektivitätengruppe einer projektiven Geraden über ${\displaystyle K}$. Die Achsenspiegelungen ${\displaystyle {\mathfrak {S}}}$ sind alle involutorischen Projektivitäten aus ${\displaystyle {\mathfrak {G}}=\operatorname {PGL} (2,K)}$ mit negativer Determinante.

Für ${\displaystyle K=\mathbb {R} }$ ist das gruppentheoretische Modell isomorph zum Kleinschen Kreisscheibenmodell. Da der Körper der reellen Zahlen nur eine Anordnung zulässt und jede hyperbolische Polarität äquivalent zur Standardbilinearform mit der Formmatrix ${\displaystyle \operatorname {diag} (1,-1,-1)}$ ist, kann man zeigen, dass das Kreisscheibenmodell die bis auf Isomorphie einzige hyperbolische Ebene (im Sinne der in diesem Artikel formulierten Axiome) über den reellen Zahlen ist.

Am reellen Beispiel lässt sich veranschaulichen, wie das gruppentheoretische Modell zustande kommt: Die Bewegungsgruppe des kleinschen Modells, das heißt die Gruppe der Kollineationen der projektiven Ebene ${\displaystyle \mathbb {P} ^{2}(\mathbb {R} )}$, die das Kreisinnere des Einheitskreises so auf sich abbilden, dass die hyperbolische Orthogonalität erhalten bleibt, besteht genau aus denjenigen Projektivitäten, die die Einheitskreislinie auf sich abbilden. Diese Untergruppe der ${\displaystyle \operatorname {PGL} (3,K)}$ ist für jeden nichtausgearteten Kegelschnitt isomorph zu ${\displaystyle \operatorname {PGL} (2,K)}$ (für formal reellen Körper ${\displaystyle K}$).

Elliptische Modelle

Die Sphärische Geometrie auf der Einheitskugel ${\displaystyle S}$ im reellen dreidimensionalen Raum, bei der einander auf ${\displaystyle S}$ gegenüberliegende Punkte („Antipoden“) miteinander identifiziert werden, wenn zusätzlich die entsprechende Orthogonalität von Großkreisen definiert wird. Siehe dazu auch Korrelation (Projektive Geometrie)#Eine elliptische Polarität. Dies ist das (bis auf Isomorphie einzige) Modell der ebenen, reellen elliptischen Geometrie.

Allgemein ist für jeden elliptischen projektiv-metrischen Raum die volle Bewegungsgruppe ${\displaystyle {\mathfrak {G}}:=O_{n+1}(K,B)}$ mit der Menge aller involutorischen Elemente dieser Gruppe als Erzeugendensystem ${\displaystyle {\mathfrak {S}}=\{a\in {\mathfrak {G}}\setminus \{1\}:a^{2}=1\}}$ ein Modell einer ${\displaystyle n}$-dimensionalen elliptischen Geometrie.^[19] Notwendig und hinreichend für die Erklärbarkeit einer elliptischen „Metrik“ im ${\displaystyle \mathbb {P} ^{n}(K)}$, mit der dieser zu einem elliptischen projektiv-metrischen Raum wird, ist die Existenz einer projektiven elliptischen Polarität auf diesem Raum.

Im Allgemeinen müssen zwei elliptische Ebenen über dem gleichen Körper nicht isomorph sein. Sie sind es dann (hinreichende Bedingung) wenn die elliptische Polarität der einen Ebene durch Wahl einer geeigneten Basis des Koordinatenvektorraums ${\displaystyle K^{n+1}}$ auf die Form gebracht werden kann, die sie auf der anderen Ebene hat.

Literatur

Originalliteratur

• Johannes Hjelmslev: Neue Begründung der ebenen Geometrie. In: Math. Ann. Band 64, 1907, S. 449–474. 
• Arnold Schmidt: Die Dualität von Inzidenz und Senkrechtstehen in der absoluten Geometrie. In: Math. Ann. Band 118, 1943, S. 609–625. 

Zur Mehrdimensionalen (n>2) Verallgemeinerung

• H. Kinder: Elliptische Geometrie endlicher Dimension. In: Arch. Math. Band 21, 1970, S. 515–527. 
• Gerhard Hübner: Klassifikation n-dimensionaler absoluter Geometrien. In: Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. Band 33, 1969, S. 165–182. 

Lehrbuch (Hauptquelle)

• Friedrich Bachmann: Aufbau der Geometrie aus dem Spiegelungsbegriff. 2. ergänzte Auflage. Springer, Berlin / Heidelberg / New York 1973, ISBN 3-540-06136-3. 

Einzelnachweise und Anmerkungen

1. ↑ Die grundlegende Idee zu einer „Spiegelungsgeometrie“ stammt von Hjelmslev, z. B. Hjelmslev (1907), Bachman hat nach seinen Worten ein Axiomensystem von Schmidt (Schmidt, 1943) „reduziert“.
2. ↑ Bachmann (1973)
3. ↑ Bachmann (1973), S. 32.
4. ↑ Formuliert man wie hier die Geometrie gruppentheoretisch, so ergibt sich, dass in der elliptischen Geometrie Punkte und Geraden als Gruppenelemente nicht zu unterscheiden sind. Trotzdem ist man bei vielen Formulierungen, in denen Senkrecht- oder Inzidenzrelationen vorkommen, formal auf der sicheren Seite, wenn man sich Punkt- und Geradenmenge „disjunkt gemacht“ denkt.
5. ↑ Aus dieser Eindeutigkeitsaussage folgt die (viel schwächere) „Einfachheit“ der Ebene als Inzidenzstruktur: Eine Gerade ist vollständig durch die Menge der mit ihr inzidierenden Punkte bestimmt. Daher genügt es, die Morphismen, hier die orthogonalen Kollineationen, als Punktabbildungen zu definieren.
6. ↑ Bachmann (1973), §3.7 Satz 18
7. ↑ Bachmann (1973), §3.7 Satz 19
8. ↑ Bachmann (1973), §4.4 Satz 6 (Transitivitätssatz)
9. ↑ Hjelmslev (1907)
10. ↑ Man beachte hier: Pol ${\displaystyle C}$ und Polare ${\displaystyle c}$ sind in der Gruppe identische Elemente, aber als geometrische Objekte nie inzident, denn ${\displaystyle cC=1}$ bedeutet, dass ${\displaystyle cC}$ keine Involution ist.
11. ↑ Bachmann (1973), §6,8, Satz 13 (Rechtseitsatz)
12. ↑ ^{a b c d} Bachmann (1973) §14.1 Die Axiome der hyperbolischen Bewegungsgruppen
13. ↑ Bachmann (1973) §6.12 Begründung der absoluten Geometrie
14. ↑ Tatsächlich muss man die Einbettungsabbildung aus mehreren Halbspiegelungen, die auf Geraden wirken und deren „gespiegelte Inverse“, die auf Punkte wirken, zusammensetzen und Polarität und Erzeugendensystem nachträglich aus den eigentlichen Objekten rekonstruieren. Die Grundidee geht auf Hjelmslev zurück. Bachmann (1973) §6.10 Begründung der metrischen Geometrie
15. ↑ Da eigentliche Idealgeraden nie mit ihrem Pol inzidieren, existiert nur eine involutorische Perspektivität mit diesen Vorgaben.
16. ↑ Bachmann (1973), §6.5 Satz 10
17. ↑ Projektiv ist jede involutorische Perspektivität mit der Ferngerade als Achse und einem eigentlichen Punkt ${\displaystyle Z}$ als Zentrum (eine eigentliche Punktspiegelung an ${\displaystyle Z}$) eine solche Achsenspiegelung. Aber zur Ferngerade existiert kein Pol.
18. ↑ Bachmann (1973), §20.9 ${\displaystyle n}$-dimensionale absolute Geometrie.
19. ↑ Kinder (1970)