Kreise am Dreieck

Wenn in der Geometrie von Kreisen am Dreieck die Rede ist, sind in erster Linie die folgenden Kreise gemeint, die schon in der Antike von griechischen Mathematikern untersucht wurden:
Umkreis
Der Umkreis eines Dreiecks ist der Kreis, der durch alle drei Ecken des gegebenen Dreiecks geht. Sein Mittelpunkt ist von den drei Ecken gleich weit entfernt und liegt daher auf allen drei Mittelsenkrechten (Streckensymmetralen).
Inkreis
Der Inkreis eines Dreiecks ist der Kreis, der alle drei Seiten des gegebenen Dreiecks im Inneren berührt, also der größte Kreis, der im Inneren des Dreiecks liegt. Der Mittelpunkt des Inkreises hat zu allen drei Seiten den gleichen Abstand und liegt folglich auf allen drei Winkelhalbierenden (Winkelsymmetralen) der Innenwinkel.
Ankreis
Ganz ähnlich definiert wie der Inkreis sind die drei Ankreise, die jeweils das Innere einer Dreiecksseite und die Verlängerungen der beiden anderen Seiten berühren. Ihre Mittelpunkte ergeben sich dadurch, dass man jeweils die Winkelhalbierende eines Innenwinkels mit den Winkelhalbierenden der nicht anliegenden Außenwinkel schneidet.
Feuerbachkreis
Ein weiterer Kreis mit interessanten Eigenschaften, die erst in der Neuzeit entdeckt wurden, ist der Feuerbach-Kreis, benannt nach Karl Wilhelm Feuerbach. Er wird auch als Neun-Punkte-Kreis bezeichnet, da auf ihm die drei Seitenmittelpunkte, die drei Fußpunkte der Dreieckshöhen und die drei Mittelpunkte der „oberen Höhenabschnitte“ (zwischen dem Höhenschnittpunkt und den Ecken) liegen. Der Mittelpunkt des Feuerbach-Kreises liegt auf der sogenannten eulerschen Geraden, die durch den Umkreismittelpunkt, den Höhenschnittpunkt und den Schwerpunkt geht. Der Radius des Feuerbachkreises ist halb so groß wie der Umkreisradius. Außerdem berührt der Feuerbach-Kreis den Inkreis und die drei Ankreise.
Siehe auch
Literatur
- Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3
Auf dieser Seite verwendete Medien
Autor/Urheber: Petrus3743, Lizenz: CC BY-SA 4.0
Malfatti-Kreise in einem ungleichseitigem Dreieck
Autor/Urheber: Oldracoon 13:04, 11 October 2012 (UTC), Lizenz: CC BY 3.0
Allgemeines Dreieck mit Umkreismittelpunkt U (blau), Schwerpunkt S (grün), Höhenschnittpunkt H (rot) und den dafür nötigen Geraden.
LamoenKreis
Autor/Urheber: de:Benutzer:Tobiasinator, Lizenz: Copyrighted free use
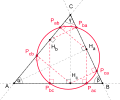
Dreieck mit Umkreis (rot), Inkreis (grün), Ankreisen (blau) und Feuerbach-Kreis (violett)
Autor/Urheber: JasperOCommons, Lizenz: CC BY-SA 3.0
Ein Dreieck mit Inkreis (grün), den drei Kreisen um die Ecken, die sich jeweils gegenseitig berühren (genau dort, wo sich Inkreis und Seiten berühren, blau) und innerem/äusserem Soddy-Kreis
Autor/Urheber: Kmhkmh, Lizenz: CC BY 4.0
johnson circles with eference triangle and johnson triangle
Autor/Urheber: Claudio Rocchini, Lizenz: CC BY-SA 3.0
Schema of Lester's theorem. X3 = circumcenter, x4 = nine-point center, X13,14 = Fermat Points. The black circle is Lester Circle.