Empirisches Quantil

Ein empirisches (${\displaystyle p}$-)Quantil, auch Stichprobenquantil oder kurz Quantil (von lat. quantillus für wie wenig?^[1]) genannt, ist in der Statistik eine Kennzahl einer Stichprobe. Für jede Zahl ${\displaystyle p}$ zwischen 0 und 1 teilt – vereinfacht dargestellt – ein empirisches ${\displaystyle p}$-Quantil die Stichprobe so, dass ein Anteil der Stichprobe von ${\displaystyle p}$ kleiner als das empirische ${\displaystyle p}$-Quantil ist und ein Anteil von ${\displaystyle 1-p}$ der Stichprobe größer als das empirische ${\displaystyle p}$-Quantil ist. Ist beispielsweise eine Stichprobe von Schuhgrößen gegeben, so ist das empirische 0,35-Quantil diejenige Schuhgröße ${\displaystyle s}$, so dass 35 % der Schuhgrößen in der Stichprobe kleiner als ${\displaystyle s}$ sind und 65 % größer als ${\displaystyle s}$ sind.

Einige empirische ${\displaystyle p}$-Quantile tragen Eigennamen. Zu ihnen gehören der Median (${\displaystyle p=0{,}5}$), das obere Quartil und das untere Quartil sowie die Terzile, Quintile, Dezile und die Perzentile.

Von den hier besprochenen empirischen Quantilen sind die Quantile (im Sinne der Wahrscheinlichkeitstheorie) zu unterscheiden. Diese sind Kennzahlen einer Wahrscheinlichkeitsverteilung und damit einer abstrakten (Mengen-)Funktion (ähnlich dem Erwartungswert), während die empirischen Quantile Kennzahlen einer Stichprobe sind (ähnlich dem arithmetischen Mittel).

Eine bekannte Darstellung und Veranschaulichung empirischer Quantile ist die Parade der Einkommen (Pen’s Parade) des Ökonomen Jan Pen zur Einkommensverteilung.

Es bezeichne ${\displaystyle \lfloor x\rfloor }$ die Abrundungsfunktion. Sie rundet jede Zahl ${\displaystyle x}$ auf die nächste kleinere ganze Zahl ab. Es gilt also beispielsweise ${\displaystyle \lfloor 1{,}2\rfloor =1}$ und ${\displaystyle \lfloor 3{,}99\rfloor =3}$.

Gegeben sei eine Stichprobe ${\displaystyle \left(x_{1},x_{2},\dotsc ,x_{n}\right)}$ der Größe ${\displaystyle n}$, deren Elemente der Größe nach geordnet sind. Dies bedeutet, es gilt

${\displaystyle x_{1}\leq x_{2}\leq \dotsb \leq x_{n}}$.

Sei ${\displaystyle p\in (0,1)}$, dann ist

${\displaystyle x_{p}={\begin{cases}{\tfrac {1}{2}}(x_{n\cdot p}+x_{n\cdot p+1}),&{\text{wenn }}n\cdot p{\text{ ganzzahlig,}}\\x_{\lfloor n\cdot p+1\rfloor },&{\text{wenn }}n\cdot p{\text{ nicht ganzzahlig.}}\end{cases}}}$

das empirische ${\displaystyle p}$-Quantil von ${\displaystyle x_{1},x_{2},\dotsc ,x_{n}}$.^[2]

Es existieren einige von der hier angegebenen Definition abweichende Definitionen.^[3]

Das Stichprobenquantil ist asymptotisch für große Stichprobenumfänge und für Stichprobenvariablen mit einer Wahrscheinlichkeitsdichte ${\displaystyle f}$ gemäß der folgenden Normalverteilung verteilt^[4] :

${\displaystyle {\text{Empirisches p-Quantil}}\sim {\mathcal {N}}\left(\mu =p,\sigma ^{2}={\frac {p(1-p)}{nf(x_{p})^{2}}}\right),}$

wobei ${\displaystyle p}$ das Quantil ist, ${\displaystyle n}$ der Stichprobenumfang und ${\displaystyle x_{p}=F^{-1}(p)}$ der Wert der Zufallsvariable beim p-Quantil.

Die folgende Stichprobe besteht aus zehn zufälligen ganzen Zahlen (gezogen aus den Zahlen zwischen null und hundert, versehen mit der diskreten Gleichverteilung):

${\displaystyle 82;\,91;\,12;\,92;\,63;\,9;\,28;\,55;\,96;\,97}$

Sortieren liefert die Stichprobe

${\displaystyle x_{1}=9;\,x_{2}=12;\,x_{3}=28;\,x_{4}=55;\,x_{5}=63;\,x_{6}=82;\,x_{7}=91;\,x_{8}=92;\,x_{9}=96;\,x_{10}=97}$.

Es ist ${\displaystyle n=10}$.

Für ${\displaystyle p=0{,}5}$ erhält man ${\displaystyle p\cdot n=5}$. Da dies ganzzahlig ist, erhält man über die Definition

${\displaystyle x_{0{,}5}={\tfrac {1}{2}}\left(x_{5}+x_{5+1}\right)={\tfrac {1}{2}}(63+82)=72{,}5}$

Für ${\displaystyle p=0{,}25}$ erhält man ${\displaystyle p\cdot n+1=0{,}25\cdot 10+1=2{,}5+1}$. Die Abrundungsfunktion liefert dann ${\displaystyle \lfloor 3{,}5\rfloor =3}$ und damit

${\displaystyle x_{0{,}25}=x_{3}=28}$.

Analog erhält man für ${\displaystyle p=0{,}75}$ direkt ${\displaystyle p\cdot n+1=0{,}75\cdot 10+1=8{,}5}$ und damit ${\displaystyle \lfloor 8{,}5\rfloor =8}$, also ist

${\displaystyle x_{0{,}75}=x_{8}=92}$.

Das empirische Quantil ist im Gegensatz zum arithmetischen Mittel robust gegenüber Ausreißern. Dies bedeutet, dass wenn man Werte einer Stichprobe oberhalb (oder unterhalb) eines bestimmten Quantils durch einen Wert oberhalb (oder unterhalb) des Quantils ersetzt, sich das Quantil selbst nicht verändert. Dies beruht darauf, dass Quantile nur durch ihre Ordnung und damit ihre Lage zueinander bestimmt werden und nicht durch die konkreten Zahlenwerte der Stichprobe. So wäre im Fall der obigen Stichprobe das arithmetische Mittel ${\displaystyle {\overline {x}}=62{,}5}$. Modifiziert man nun aber den größten Wert der Stichprobe, setzt beispielsweise

${\displaystyle x_{10}=1000}$,

so ist ${\displaystyle {\overline {x}}=152{,}8}$, wohingegen der Median sowie das untere und das obere Quartil unverändert bleiben, da sich die Reihenfolge der Stichprobe nicht verändert hat.

Für gewisse ${\displaystyle p}$-Werte tragen die zugehörigen Quantile Eigennamen. Sie sind hier im Folgenden kurz vorgestellt. Zu beachten ist, dass auch die entsprechenden Quantile von Wahrscheinlichkeitsverteilungen teils mit denselben Eigennamen bezeichnet werden.

Der Median ist das ${\displaystyle 0{,}5}$-Quantil und teilt somit die Stichprobe in zwei Hälften: Eine Hälfte ist kleiner als der Median, die andere größer als der Median. Er ist mit dem Modus und dem arithmetischen Mittel ein wichtiger Lageparameter in der deskriptiven Statistik.

Als Terzile werden die beiden ${\displaystyle p}$-Quantile für ${\displaystyle p={\tfrac {1}{3}}}$ und ${\displaystyle p={\tfrac {2}{3}}}$ bezeichnet. Sie teilen die Stichprobe in drei gleich große Teile: ein Teil ist kleiner als das untere Terzil (=${\displaystyle {\tfrac {1}{3}}}$-Quantil), ein Teil ist größer als das obere Terzil (=${\displaystyle {\tfrac {2}{3}}}$-Quantil), und ein Teil liegt zwischen den Terzilen.

Als Quartile werden die beiden Quantile mit ${\displaystyle p=0{,}25}$ und ${\displaystyle p=0{,}75}$ bezeichnet. Dabei heißt das ${\displaystyle 0{,}25}$-Quantil das untere Quartil und das ${\displaystyle 0{,}75}$-Quantil das obere Quartil. Zwischen oberem und unterem Quartil liegt die Hälfte der Stichprobe, unterhalb des unteren Quartils und oberhalb des oberen Quartils jeweils ein Viertel der Stichprobe. Auf Basis der Quartile wird der Interquartilsabstand definiert, ein Streuungsmaß.

Als Quintile werden die vier Quantile mit ${\displaystyle p=0{,}2;\,0{,}4;\,0{,}6;\,0{,}8}$ bezeichnet. Demnach befinden sich 20 % der Stichprobe unter dem ersten Quintil und 80 % darüber, 40 % der Stichprobe unter dem zweiten Quintil und 60 % darüber etc.

Die Quantile für Vielfache von ${\displaystyle 0{,}1}$, also für ${\displaystyle p=0{,}1;\,0{,}2;\,\dotsc ;\,0{,}9}$ werden Dezile genannt. Dabei heißt das ${\displaystyle 0{,}1}$-Quantil das erste Dezil, das ${\displaystyle 0{,}2}$-Quantil das zweite Dezil etc. Unterhalb des ersten Dezils liegen 10 % der Stichprobe, oberhalb entsprechend 90 % der Stichprobe. Ebenso liegen 40 % der Stichprobe unterhalb des vierten Dezils und 60 % oberhalb.

Als Perzentile werden die Quantile von ${\displaystyle 0{,}01}$ bis ${\displaystyle 0{,}99}$ in Schritten von ${\displaystyle 0{,}01}$ bezeichnet.

Aus den Quantilen lassen sich noch gewisse Streuungsmaße ableiten. Das wichtigste ist der Interquartilabstand (englisch interquartile range)

${\displaystyle {\text{IQR}}:=x_{0{,}75}-x_{0{,}25}}$.

Er gibt an, wie weit das obere und das untere Quartil auseinanderliegen und damit auch, wie breit der Bereich ist, in dem die mittleren 50 % der Stichprobe liegen.^[5] Etwas allgemeiner kann der (Inter-)quantilabstand definiert werden als ${\displaystyle x_{1-p}-x_{p}}$ für ${\displaystyle p\in (0;0{,}5)}$. Er gibt an, wie breit der Bereich ist, in dem die mittleren ${\displaystyle 100\cdot (1-2p)\,\%}$ der Stichprobe liegen. Für ${\displaystyle p=0{,}25}$ entspricht er dem Interquartilabstand.

Ein weiteres abgeleitetes Streumaß ist die mittlere absolute Abweichung vom Median.

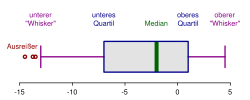
Eine Möglichkeit, Quantile darzustellen, ist der Box-Plot. Dabei wird die gesamte Stichprobe durch einen Kasten – versehen mit zwei Antennen – dargestellt. Die äußere Begrenzung des Kastens sind jeweils das obere und das untere Quartil. Somit befindet sich die Hälfte der Stichprobe im Kasten. Der Kasten selbst ist nochmals unterteilt, der unterteilende Strich ist dabei der Median der Stichprobe. Die Antennen sind nicht einheitlich definiert. Eine Möglichkeit ist, als Begrenzung der Antennen das erste und das neunte Dezil zu wählen.

1. ↑ Herkunft des Begriffs laut Duden
2. ↑ Norbert Henze: Stochastik für Einsteiger. Eine Einführung in die faszinierende Welt des Zufalls. 10. Auflage. Springer Spektrum, Wiesbaden 2013, ISBN 978-3-658-03076-6, S. 30, doi:10.1007/978-3-658-03077-3. 
3. ↑ Eric W. Weisstein: Quantile. In: MathWorld (englisch).
4. ↑ Alan Stuart, Keith Ord: Kendall's Advanced Theory of Statistics. Arnold, London 1994, ISBN 0-340-61430-7. 
5. ↑ Eric W. Weisstein: Interquartile Range. In: MathWorld (englisch).