Downhill-Simplex-Verfahren
Das Downhill-Simplex-Verfahren oder Nelder-Mead-Verfahren[1] ist im Unterschied zum Namensvetter für lineare Probleme (Simplex-Algorithmus) eine Methode zur Optimierung nichtlinearer Funktionen von mehreren Parametern. Er fällt in die Kategorie der Hillclimbing- oder Downhill-Suchverfahren. Angewendet werden kann er z. B. auch beim Kurvenfitten.
Es wurde von John Nelder und Roger Mead 1965 eingeführt.
Grundlagen

Als Besonderheit kommt dieser Simplex-Algorithmus ohne Ableitungen der Funktion nach den Parametern aus, welche bei manchen Problemstellungen nicht mit vertretbarem Aufwand berechenbar sind. Durch sinnvolle Vergleiche der Funktionswerte mehrerer Punkte im Parameterraum wird ähnlich wie bei einer Regula falsi mit Schrittweitensteuerung die Tendenz der Werte und der Gradient Richtung Optimum angenähert. Das Verfahren konvergiert nicht extrem schnell, ist aber dafür einfach und relativ robust.
Der Algorithmus basiert auf einem Simplex, dem einfachsten Volumen im -dimensionalen Parameterraum, das aus Punkten aufgespannt wird. Im Eindimensionalen auf der Zahlengeraden ist das eine Strecke, im Zweidimensionalen ein Dreieck usw. Jeder Punkt entspricht dabei einem (Koordinaten-)Satz Parameter (bzw. Variablen), und zu jedem Punkt kann man einen Funktionswert berechnen, den man z. B. als Fehler- oder Kostenwert ansehen kann. Unter diesen Punkten ermittelt man dann den „schlechtesten“ und den „besten“. Von einem Iterationsschritt zum nächsten wird normalerweise der „schlechteste“ dieser Punkte durch einen neuen ersetzt, der hoffentlich „besser“ ist. Den „besten“ Punkt behält man als bisher beste Lösung immer bei.
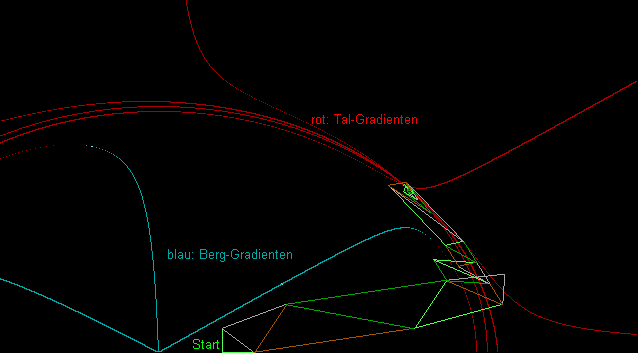
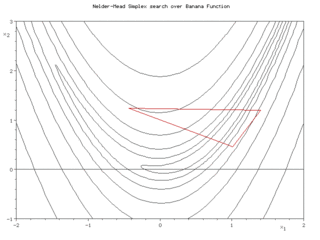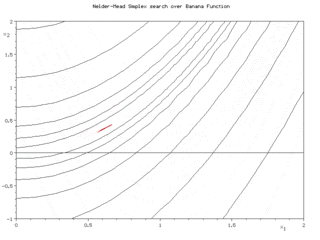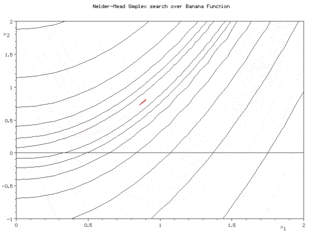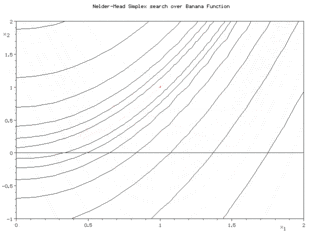
Bei einer Visualisierung im Zweidimensionalen mit Höhenlinien für die zu optimierende Funktion sieht man (in den Bildern rechts) ein Dreieck, das sich zielstrebig dem Optimum nähert, indem es sich um eine seiner Seiten klappt, sich streckt oder in der Nähe des Optimums um dieses zusammenzieht. Siehe auch die Abbildung ganz unten.
Ohne Ableitungen entfallen diverse Fallen wie pathologisches Verhalten dieser Ableitungen bei Unstetigkeiten, sodass das Verfahren zwar im Allgemeinen langsamer konvergiert (nämlich linear) als Optimierungsverfahren mit Ableitungen, aber wesentlich robuster arbeitet. Die möglichen Fallen beim Simplex-Verfahren sind ähnlich wie bei den meisten Optimierungsverfahren unverhoffte lokale Nebenminima (bzw. -optima), auf die konvergiert werden kann, oder dass das Verfahren sich für einen oder mehrere Parameter zu früh auf einen konstanten Wert zusammenzieht.
Algorithmus

Das Downhill-Simplex-Verfahren findet ein lokales Optimum einer Funktion mit Variablen (Parametern). Gegeben ist eine Zielfunktion , die jedem Punkt im Lösungsraum einen Wert (Qualität der Lösung) zuordnet. sind Parameter des Algorithmus.
- wähle Anfangspunkte , die den Simplex bilden
- sortiere die Punkte nach dem Wert der Zielfunktion , so dass der beste, der zweitschlechteste und der schlechteste ist
- bilde von allen außer dem schlechtesten Punkt den Mittelpunkt:
- reflektiere den schlechtesten Punkt am Mittelpunkt:
- wenn besser ist als : bestimme den expandierten Punkt , ersetze durch den besseren der beiden Punkte und gehe zu Schritt 2
- wenn besser ist als der zweitschlechteste Punkt : ersetze durch und gehe zu Schritt 2
- sei der bessere der beiden Punkte . Bestimme den kontrahierten Punkt
- wenn besser ist als : ersetze durch und gehe zu Schritt 2
- komprimiere den Simplex: für jedes : ersetze durch
- gehe zu Schritt 2
Nach diesen Regeln wird die Iteration so lange weitergeführt, bis ein Konvergenzkriterium erfüllt ist. Der Simplex wird sich dabei in Richtung eines lokalen Optimums verlagern und sich schließlich um dieses herum zusammenziehen.
| Parameter | sinnvoller Bereich | typischer Wert |
|---|---|---|
| (Reflexion) | ||
| (Expansion) | ||
| (Kontraktion) | ||
| (Komprimierung) |
Die Anfangspunkte müssen so gewählt werden, dass sie einen Simplex der Dimension aufspannen und nicht alle in einer Hyperebene von kleinerer Dimension liegen, d. h. die Vektoren müssen linear unabhängig sein. Man kann z. B. einen Punkt als Startpunkt wählen und weitere ermitteln, indem man von diesem aus jeweils einen der Parameter um einen von 1 verschiedenen Faktor (falls der Parameter nicht 0 sein kann) oder einen von 0 verschiedenen Summanden erhöht. Alternativ: Man gibt für jeden Parameter zwei verschiedene Werte vor, berechnet den ersten Punkt mit allen Erstwerten und die anderen Punkte auch mit den Erstwerten, nur dass jeweils einer der Parameter durch seinen Zweitwert ersetzt wird. Oder man wählt Zufallspunkte aus dem Lösungsraum.
Grafische Darstellung eines Beispiellaufs

Das Bild zeigt das Ergebnis eines Programmlaufs. Die roten und blauen Linien stellen die Gefällelinien für Täler bzw. Berge dar. Es handelt sich um einen Kreisgraben in einer schrägen Ebene, es interessiert hier das lokale Minimum innerhalb des Kreisgrabens. Die Simplex-Iteration findet das Minimum an der Kreuzungsstelle der roten Linien. In - und -Richtung reicht die Grafik von 0 bis 4.
Erweiterungen für Notfälle
Wie bei anderen Verfahren besteht immer die Gefahr, dass auf ein Nebenoptimum konvergiert wird. Diese Gefahr kann man durch mehrere Maßnahmen mindern:
- Nach einer bestimmten Anzahl von Schritten wird neu angesetzt. Dazu wird der bisher beste Punkt beibehalten und um ihn herum ein neuer Start-Simplex aufgebaut, indem bei jedem weiteren Punkt die Koordinate (nur) eines Parameters z. B. um 5 % variiert wird.
- Genau wie eben, nur werden die zusätzlichen Simplex-Punkte durch Zufallswerte noch mehr flexibilisiert.
- Statt solche Maßnahmen nach einer festen Anzahl von Schritten zu ergreifen, kann man den Zeitpunkt auch vom aktuellen Stand der Iteration abhängig machen. Dazu muss das Problem natürlich besser bekannt sein, dass man sich dessen auch sicher sein kann.
- Alternativ kann man sogar den Zeitpunkt der Neuansetzung per Zufallszahl variabel gestalten.
- Eine zusätzliche Sicherheitsabfrage könnte den Fall abfangen, dass sich nur einer der Parameter vorzeitig festgelaufen hat, dann könnte man ihm eine Spezialbehandlung zukommen lassen.
All diese Varianten erfordern eine intensive Beschäftigung mit dem jeweiligen konkreten Problem, es gibt leider keine allgemein gültigen Kochrezepte dafür.
Erweiterung zum Kurvenfitten
Will man nicht eine einzelne analytische Funktion von Parametern (Koordinaten) optimieren, sondern eine Theoriefunktion an eine Messkurve anpassen, ist nur ein kleiner zusätzlicher Schritt notwendig: Als zu optimierende Funktion verwendet man oft die Fehlerquadratsumme, also die Summe aus den Quadraten der Differenzen aus den einzelnen Messwerten (Kurvenpunkten) und den Theoriefunktionswerten an denselben Stellen, wobei letztere einerseits von der -Koordinate der Messkurve abhängen und zusätzlich von den Parametern. Ob man aus der Fehlerquadratsumme noch die Wurzel zieht, ist für das Simplex-Verfahren irrelevant. Siehe hierzu auch Methode der kleinsten Quadrate.
Jedoch ist das Downhill-Simplex-Verfahren sehr flexibel (anders als etwa der Levenberg-Marquardt-Algorithmus), man kann also je nach Situation auch andere Funktionen zur Optimierung verwenden:
- Die Daten haben eine starke Streuung: Statt der Summe der quadrierten Abweichung minimiert man die Summe der Beträge der Abweichungen. Ausreißer beeinflussen das Ergebnis weniger.
- Kurvenanpassung arbeitet normalerweise mit der Annahme, dass der Fehler der abhängigen Variable unabhängig von der zugehörigen unabhängigen Variable ist (Homoskedastizität). In manchen Fällen ist jedoch eine Funktion von . Diese Situation tritt insbesondere dann auf, wenn sich und über mehrere Größenordnungen erstrecken. Würde man in solchen Fällen die Fehlerquadratsumme minimieren, bekäme man eine gute Anpassung bei großen -Werten, aber eine sehr schlechte bei kleinen, die zur Fehlerquadratsumme kaum beitragen. In solchen Fällen minimiert man , also die Summe der quadrierten relativen Abweichungen .
Beispielimplementierung
// Deklarationen
// Benutzervorgaben, -eingaben
int NP= ... ; // Anzahl der Parameter, die in FQS() eingehen,
// auch "Dimension des Parameterraums"
double ParP[NP]={ ... }; // primärer Parametersatz
double ParS[NP]={ ... }; // sekundärer Parametersatz, gibt Schwankungsbreite vor
double FQS(int pf) // Zu minimierende Funktion, hängt
{ // von den Parametern Par0[pf][...] ab.
... // Muss je nach Problemstellung erstellt werden.
// So schreiben, dass sie für den Parametersatz Nr. pf
} // berechnet und am Schluss in Par0[pf][0] (s. u.)
// abgespeichert wird.
// Ende Benutzervorgaben
// Initialisierung
// Simplex-Parameter double NA = 1, NB = .5, NC = 2; // Alpha, Beta, Gamma
// Parametersätze, NP+1 Stück für den Simplex selbst, plus 3 weitere double Par0[NP+4][NP+1]; // darin 1. Index: 0..NP die (NP+1) Parametersätze des Simplex, // dabei auf 0 immer der schlechteste Punkt des Simplex, // auf 1 immer der beste Punkt des Simplex // NP+1 Punkt P*, s. u. // NP+2 Punkt P**, s. u. // NP+3 Mittelpunkt P-Quer des Simplex, s. u. // darin 2. Index: 0 Fehlerwert für diesen Satz // 1..NP einzelne Parameterwerte dieses Satzes
// Initialisierung
// Simplex aus Primär- und Sekundärwerten Parametersätze 0 bis NP mit Primärwerten belegen; In Parametersätzen 1 bis NP (i) jeweils Parameter Nr. i mit Sekundärwert belegen;
// Berechnung der Anfangs-Fehlersummen für Parametersätze 0 bis NP: feh=FQS(i); // speichert Ergebnis in Par0[i][0], s. o.
// Schleife für Iteration, Hauptschleife
bool fertig = false;
while (!fertig)
NT++; // Simplex-Schritt Nr. NT
// schlechtesten und besten Punkt ermitteln (höchster bzw. niedrigster Fehlerwert)
Werte fmin und fmax auf Fehlerwert von Satz Nr. 0 vorbelegen;
für alle Parametersätze von 1 bis NP:
wenn Fehler für Satz Nr. i größer als fmax:
noch schlechterer Punkt, fmax auf diesen Wert, Punkt mit Nr. 0 tauschen
wenn Fehler für Satz Nr. i kleiner als fmin:
noch besserer Punkt, fmin auf diesen Wert, Punkt mit Nr. 1 tauschen
// Konvergenzabfrage, sind wir fertig?
// Dies muss auch je nach Problem individuell erstellt werden,
// hier als Beispiel die Bedingung, dass alle Parameter nur noch um 1 ‰
// schwanken.
fertig = true;
für alle Parameter in allen Parametersätzen von 0 bis NP:
wenn nur für einen Parameter die relative Abweichung des Wertes
zwischen schlechtestem und bestem Punkt größer als 0.001, dann:
fertig=false; // doch noch nicht fertig
//Wenn fertig, dann beende mit bestem Punkt Par0[1][1..3] als Ergebnis des Algorithmus
// Mittelpunkt P-QUER des Simplex nach Index NP+3
Mittelwerte über Sätze 1 bis NP (also ohne schlechtesten Punkt Nr. 0!) bilden
und als Satz Nr. NP+3 speichern;
// Punkt P* durch Reflexion des schlechtesten Punkts
// am Mittelpunkt P-QUER (mit Nelder/Mead-Parameter alpha=NA) nach Index NP+1
innerhalb eines Parametersatzes:
Par0[NP+1][i]=(1 + NA) * Par0[NP+3][i] - NA * Par0[0][i];
fs=Par0[NP+1][0]=FQS(NP+1); // und Fehler berechnen
// Fallunterscheidung, ob Verbesserung erreicht
wenn fs<fmin // neuer Punkt P* im Vergleich zu bisher bestem
/ // ja, besser!
| // weiteren Schritt zu Punkt P** in dieselbe Richtung nach Index NP+2
| // (mit Nelder/Mead-Parameter gamma=NC)
| innerhalb eines Parametersatzes:
| Par0[NP+2][i]=(1 + NC) * Par0[NP+1][i] - NC * Par0[NP+3][i];
| fs=Par0[NP+2][0]=FQS(NP+2); // und Fehler berechnen
|
| wenn fs>=fmin // wieder Vergleich mit bisher bestem Punkt
| / // keine weitere Verbesserung: P** verwerfen, P* nach Index 0,
| | // also bisher schlechtesten Wert durch neuen (etwas besseren) ersetzen
| \ Parametersatz Nr. NP+1 nach Nr. 0 kopieren;
| else // von fs>=fmin
| / // ja, auch eine Verbesserung!
| | // auch besser als P* ?
| | wenn fs>Par0[NP+1][0]
| | / // nein, P* weiterverwenden und damit bisher schlechtesten auf Index 0 ersetzen
| | \ Parametersatz Nr. NP+1 nach Nr. 0 kopieren;
| | else // von fs>Par0[NP+1][0]
| | / // ja, P** weiterverwenden und damit bisher schlechtesten auf Index 0 ersetzen
\ \ \ Parametersatz Nr. NP+2 nach Nr. 0 kopieren;
else // von fs<fmin
/ // nicht besser als bisher bester, nun prüfen, ob P* wenigstens überhaupt eine Verbesserung
| wenn fs von P* für wenigstens einen der Punkte 2..NP kleiner ist, dann:
| / // ja, besser als mindestens einer, mit P* den bisher schlechtesten Punkt auf Index 0 ersetzen
| \ Parametersatz Nr. NP+1 nach Nr. 0 kopieren;
| else // von fs von P*
| / // nein, weiterhin schlechter als die anderen Punkte
| | // Zusatzprüfung: sogar schlechter als bisher schlechtester Punkt fmax?
| | wenn fs>fmax // schlechter als bisher schlechtester?
| | // ja, erstmal nichts tun
| | else // von fs>fmax
| | / // nein, also wenigstens bisher schlechtesten Punkt damit ersetzen
| \ \ Parametersatz Nr. NP+1 nach Nr. 0 kopieren;
| // neuer Punkt P** durch Kontraktion zwischen bisher schlechtestem Punkt (Index 0)
| // und P-QUER (Index NP+3) nach Index NP+2 (mit Nelder/Mead-Parameter beta=NB)
| innerhalb eines Parametersatzes:
| Par0[NP+2][i]= NB * Par0[0][i] + (1 - NB) * Par0[NP+3][i];
| fs=Par0[NP+2][0]=FQS(NP+2); // und Fehler berechnen
| // P** besser als bisher schlechtester Punkt?
| wenn fs<fmax // besser als bisher schlechtester?
| / // ja, bisher schlechtesten durch P** ersetzen
| \ Parametersatz Nr. NP+2 nach Nr. 0 kopieren;
| else // von fs<fmax
| / // nein, keinerlei Verbesserung, Notfall
| | // folgt allgemeine Kompression um Faktor 2 um den bisher besten Punkt herum
| | für alle Parametersätze außer Nr. 1 (bisher bester): // also j=0 und 2..NP
| | innerhalb eines Parametersatzes j:
| | Par0[j][i]=(Par0[j][i] + Par0[1][i]) / 2;
\ \ fs=Par0[j][0]=FQS(j); // und Fehler berechnen
// Schleifenende
Literatur
- Jeffrey C. Lagarias, James A. Reeds, Margaret H. Wright, Paul E. Wright: Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. In: SIAM Journal on Optimization. Band 9, Nr. 1, 1998, S. 112–147, doi:10.1137/S1052623496303470.
- Larry Nazareth, Paul Tseng: Gilding the Lily: A variant of the Nelder-Mead algorithm based on Golden-Section Search. Computational Optimization and Applications, Bd. 22 (2002), Nr. 1, S. 133–144
- Jeffrey C. Lagarias, Bjorn Poonen, Margaret H. Wright: Convergence of the restricted Nelder-Mead algorithm in two dimensions. SIAM J. Optimization 22 (2012), Nr. 2, S. 501–532
- William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery: Numerical Recipes in C. Foundation Books 2007, ISBN 978-81-85618-16-6.
- John Ashworth Nelder, Roger Mead: A Simplex Method for Function Minimization. Computer Journal, 1965, 7, 308–313 (Originaltext als PDF-Datei, 543 kB)
- Marco A. Luersen, Rodolphe Le Riche: Globalized Nelder–Mead method for engineering optimization. Computers and Structures 82 (2004), S. 2251–2260
- David Byatt, Ian Coope, Chris Price: 40 years of the Nelder-Mead algorithm (PDF-Datei; 3,46 MB)
- Saša Singer, Sanja Singer: Efficient implementation of the Nelder-Mead search algorithm. Applied Numerical Analysis and Computational Mathematics, Bd. 1 (2004), Nr. 2, S. 524–534 (Zusammenfassung)
- Andrej Prša, Tomaž Zwitter: Introducing adapted Nelder & Mead's downhill simplex method to a fully automated analysis of eclipsing binaries. In: C. Turon, K. S. O’Flaherty, M. A. C. Perryman (Hrsg.): The Three-Dimensional Universe with Gaia (ESA SP-576). Proc. Gaia Sympos. 2004, ESA Publications Division, Nordwijk 2005, S. 611–614
- Fuchang Gao, Lixing Han: Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Computational Optimization and Applications 51 (2012), Nr. 1, S. 259–277
Einzelnachweise
- ↑ Nelder, Mead A simplex method for function minimization, Computer Journal, Band 7, 1965, S. 308–313
Auf dieser Seite verwendete Medien
Autor/Urheber: Original uploader was Simiprof at en.wikipedia, Lizenz: CC BY-SA 3.0
Nelder Mead Animated gif generated by P.A. Simionescu and contributed to Wikipedia.
Autor/Urheber:
Jade Yu Cheng
Thomas Mailund, Lizenz: CC BY 4.0An iteration of the Nelder-Mead method over two-dimensional space, showing point p min reflected to point p r , expanded to point p e , or contracted to point p c. If these test points do not improve the overall score of the simplex, then it shrinks around the point p max with the highest score.
Darstellung eines Beispiellaufs des Downhill-Simplex-Verfahrens nach Nelder/Mead mit dem eingebauten Beispiel
Autor/Urheber: Original uploader was Simiprof at en.wikipedia, Lizenz: CC BY-SA 3.0
Nelder Mead Animated gif generated by P.A. Simionescu and contributed to Wikipedia.
Flowchart des Downhill-simplex-Verfahrens nach Nelder und Mead. Latex/TikZ/PGF-Quellcode ist auf der Diskussionsseite.