Deterministischer endlicher Automat

Ein deterministischer endlicher Automat (DEA; englisch deterministic finite state machine oder deterministic finite automaton, DFA) ist in der theoretischen Informatik ein endlicher Automat, der unter Eingabe eines Zeichens seines Eingabealphabetes (den möglichen Eingaben) von einem Zustand, in dem er sich befindet, in einen eindeutig bestimmten Folgezustand wechselt. Von jedem (Final-)Zustand ${\displaystyle q_{n}\in F\cup Q}$ muss für jedes Zeichen des Eingabealphabets ${\displaystyle \Sigma }$ ein Übergang in einen Folgezustand existieren.^[1] Er unterscheidet sich darin von nichtdeterministischen endlichen Automaten, deren Zustandswechsel sich nicht immer deterministisch ereignen müssen.

Definition

Automat

Formal kann ein DEA ${\displaystyle {\mathfrak {A}}}$ als Quintupel (5-Tupel) ${\displaystyle {\mathfrak {A}}=\left(Q,\,\Sigma ,\,\delta ,\,q_{0},\,F\right)}$ definiert werden. Hierbei gilt Folgendes:

• ${\displaystyle Q}$ ist eine endliche Zustandsmenge. Weitere oft verwendete Symbole für ${\displaystyle Q}$ sind ${\displaystyle Z}$ oder ${\displaystyle S}$.
• ${\displaystyle \Sigma }$ ist das endliche Eingabealphabet, also die Menge erlaubter Eingabesymbole.
• ${\displaystyle \delta \colon Q\times \Sigma \rightarrow Q}$ ist die Übergangsfunktion (oder Transitionsfunktion). Sie ordnet jedem Paar bestehend aus einem Zustand ${\displaystyle q\in Q}$ und einem Eingabesymbol ${\displaystyle a\in \Sigma }$ einen Nachfolgezustand ${\displaystyle p\in Q}$ zu.
• ${\displaystyle q_{0}\in Q}$ ist der Startzustand (auch Anfangszustand oder Initalzustand).
• ${\displaystyle F\subseteq Q}$ ist die Menge der akzeptierenden Zustände, die sogenannten Finalzustände (oder Endzustände). Ein anderes übliches Symbol für ${\displaystyle F}$ ist ${\displaystyle A}$.

Verhalten

Befindet sich der Automat ${\displaystyle {\mathfrak {A}}=\left(Q,\,\Sigma ,\,\delta ,\,q_{0},\,F\right)}$ in einem Zustand ${\displaystyle q\in Q}$ und liest das Eingabesymbol ${\displaystyle a\in \Sigma }$, wechselt er in einen neuen Zustand, der durch die Übergangsfunktion vorgegeben ist, also in den Zustand ${\displaystyle \delta (q,\,a)}$.

Hat der Automat noch kein Eingabesymbol gelesen, befindet er sich im Startzustand ${\displaystyle q_{0}}$. Erhält der Automat als Eingabe eine Folge von Eingabesymbolen, in der theoretischen Informatik Wort genannt, liest er von links nach rechts ein Symbol nach dem anderen und wechselt gemäß der Übergangsfunktion den Zustand. Befindet sich der Automat nach dem Lesen des letzten Eingabesymbols in einem akzeptierenden Zustand ${\displaystyle q_{f}\in F}$, akzeptiert er die Eingabe. Man sagt dann, dass sich das Eingabewort in der Menge der Wörter befindet, die vom Automaten akzeptiert werden (kurz: die vom Automaten akzeptierte Sprache, siehe unten).

Verworfene Eingaben

Endet der Automat nach dem Lesen eines Eingabewortes in einem nicht-akzeptierenden Zustand, gilt die Eingabe als verworfen. Wenn die Frage, ob die Eingabe verworfen oder akzeptiert wird, sich nicht erst mit dem letzten Eingabesymbol klärt, befindet sich ein minimaler Automat vorzeitig in einem Zustand, den er nicht mehr verlässt.

Sprache eines DEA

Die Menge aller vom DEA ${\displaystyle {\mathfrak {A}}}$ akzeptierten Wörter wird als Sprache ${\displaystyle {\mathcal {L}}({\mathfrak {A}})}$ von ${\displaystyle {\mathfrak {A}}}$ bezeichnet. Die Menge aller Sprachen, die von irgendeinem DEA akzeptiert werden, ist die Klasse der regulären Sprachen.

Nichtdeterministische endliche Automaten (NEA), DEA und Typ-3-Grammatiken (in der Chomsky-Hierarchie) beschreiben die gleiche Sprachklasse. NEA lassen sich mittels Potenzmengenkonstruktion in äquivalente DEA wandeln.

Beispiele

Getränkeautomat

Ein deterministischer endlicher Automat, der einfache Abläufe eines Getränkeautomaten nachbildet, kann aus den Zuständen ${\displaystyle Q=\{q_{0},q_{1},q_{2}\}}$ bestehen, welche folgende Zustände des Getränkeautomaten beschreiben: „Getränkeautomat wartet auf Münzeinwurf“, „Getränkeautomat wartet auf Getränkewahl“ und „Getränk wird ausgeschenkt“.

Gültige Eingabesymbole könnten durch die Menge ${\displaystyle \Sigma =\{{\text{Münze}},{\text{Getränk}},{\text{Abbruch}},{\text{Entnahme}}\}}$ das Einwerfen einer Münze, die Wahl eines Getränks, das Abbrechen der Getränkewahl und die Entnahme eines Getränks beschreiben.

Ein Automat mit den Übergängen

• ${\displaystyle \delta (q_{0},{\text{Münze}})=q_{1}}$,
• ${\displaystyle \delta (q_{1},{\text{Getränk}})=q_{2}}$,
• ${\displaystyle \delta (q_{2},{\text{Entnahme}})=q_{0}}$ und
• ${\displaystyle \delta (q_{1},{\text{Abbruch}})=q_{0}}$

beschreibt dann, dass zunächst mit einer Münze bezahlt wird, anschließend ein Getränk gewählt wird, welches entnommen werden muss, bevor wieder von vorne begonnen werden kann. Hat man die Münze eingeworfen, aber noch kein Getränk ausgewählt, kann man auch noch abbrechen.

Verlangt man für die Übergänge eine totale Funktion, muss unter anderem auch ein Zustand angegeben werden, in den der Automat bei Abbruch wechselt, wenn ein Getränk bereits gewählt aber noch nicht entnommen wurde.

• 

  Grafische Darstellung des DEA aus dem Beispiel

• 

  Der entsprechende DEA mit totaler Übergangsfunktion

Regulärer Ausdruck

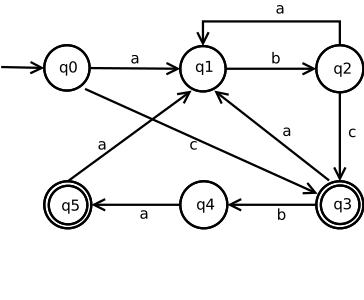
Der reguläre Ausdruck ${\displaystyle ((ab)^{*}c(ba\mid \varepsilon ))^{+}}$ kann als folgender DEA dargestellt werden:

• Zustandsmenge ${\displaystyle Q=\{q_{0},q_{1},q_{2},q_{3},q_{4},q_{5}\}}$
• Eingabealphabet ${\displaystyle \Sigma =\{a,b,c\}}$
• partielle Übergangsfunktion ${\displaystyle \delta \colon Q\times \Sigma \rightarrow Q}$ mit
  • ${\displaystyle \delta (q_{0},a)=q_{1}}$
  • ${\displaystyle \delta (q_{0},c)=q_{3}}$
  • ${\displaystyle \delta (q_{1},b)=q_{2}}$
  • ${\displaystyle \delta (q_{2},a)=q_{1}}$
  • ${\displaystyle \delta (q_{2},c)=q_{3}}$
  • ${\displaystyle \delta (q_{3},a)=q_{1}}$
  • ${\displaystyle \delta (q_{3},b)=q_{4}}$
  • ${\displaystyle \delta (q_{4},a)=q_{5}}$
  • ${\displaystyle \delta (q_{5},a)=q_{1}}$
• Finalzustände ${\displaystyle F=\{q_{3},q_{5}\}}$

• 

  Grafische Darstellung des DEA aus dem Beispiel

Minimierung

Zu jedem DEA existiert ein (bis auf die Benennung der Zustände) eindeutiger minimaler Automat, der dieselbe Sprache akzeptiert.

Da die Zustände des Minimalautomaten den Äquivalenzklassen der vom endlichen Automaten ${\displaystyle {\mathfrak {A}}}$ akzeptierten Sprache unter der Nerode-Relation entsprechen, spricht man auch vom Äquivalenzklassenautomat:

${\displaystyle u\sim _{L({\mathfrak {A}})}v\Longleftrightarrow (\forall w\in \Sigma ^{*}:uw\in L({\mathfrak {A}})\Leftrightarrow vw\in L({\mathfrak {A}}))}$

Sei ${\displaystyle {\mathfrak {A}}=(Q,\Sigma ,\delta ,q_{0},F)}$ ein deterministischer endlicher Automat. Dann ist ${\displaystyle {\mathfrak {B}}=(Q',\Sigma ,\delta ',q_{0}',F')}$ mit

• ${\displaystyle Q'={\Big \{}[w]_{L({\mathfrak {A}})}\mid w\in \Sigma ^{*}{\Big \}}}$
• ${\displaystyle ~q'_{0}=[\epsilon ]_{L({\mathfrak {A}})}}$
• ${\displaystyle ~\delta '([u]_{L({\mathfrak {A}})},a)=[ua]_{L({\mathfrak {A}})}}$
• ${\displaystyle F'={\Big \{}[u]_{L({\mathfrak {A}})}\mid u\in L({\mathfrak {A}}){\Big \}}}$

der Äquivalenzklassenautomat zu ${\displaystyle {\mathfrak {A}}}$.

Die Minimierung eines deterministischen Automaten kann algorithmisch durch fortwährende Verfeinerung der Äquivalenzklassen gelöst werden. Man beginnt mit den Zustandsmengen ${\displaystyle F}$ und ${\displaystyle Q-F}$. Für jeden Buchstaben aus dem Alphabet wird nun jede Zustandsmenge dahingehend aufgeteilt, dass die Überführungsfunktion die Zustände jeder neuen Menge den Buchstaben in eine jeweils eindeutige Menge abbildet. Dies wird so oft wiederholt bis sich keine Änderung mehr ergibt.

Es besteht außerdem die Möglichkeit, minimale deterministische endliche Automaten inkrementell aufzubauen. Inkrementell bedeutet hier, dass die zu akzeptierenden Worte einzeln dem Automaten hinzugefügt werden. Nach jedem Einfügen eines solchen Wortes ist der deterministische endliche Automat minimal. Dieses Verfahren ist vor allem dann erfolgversprechend, wenn die Worte häufig gemeinsame Prä- und Suffixe teilen, dies ist z. B. bei Worten aus natürlichen Sprachen der Fall.

Siehe auch

• Zweiwege-DFA
• Eindeutiger endlicher Automat
• Potenzautomat

Literatur

• Gottfried Vossen, Kurt Ulrich Witt: Grundkurs Theoretische Informatik. 3. Auflage. ISBN 3-528-23147-5
• Jan Daciuk, Bruce W. Watson, Richard E. Watson, Ul. G. Narutowicza: Incremental Construction of Minimal Acyclic Finite State Automata and Transducers. 1998.
• Uwe Schöning: Ideen der Informatik, Grundlegende Modelle und Konzepte. Oldenbourg, München 2006, ISBN 3-486-57833-2
• Peter Sander, Wolffried Stucky, Rudolf Herschel: Automaten, Sprachen, Berechenbarkeit. Teubner, Stuttgart 1992, ISBN 3-519-02937-5
• John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman: Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie. 2. Auflage. Pearson Studium, Reading 2002, ISBN 3-8273-7020-5

Weblinks

• Automatonsimulator – ein webbasierter, grafischer Editor und Simulator (englisch)

Einzelnachweise

1. ↑ Hans Werner Lang: Konstruktion eines deterministischen endlichen Automaten. Hochschule Flensburg, 2007, abgerufen am 9. September 2018.