Chemische Bindung

Die Chemische Bindung ist eine der wichtigsten Grundlagen der Chemie, denn die Bildung von Bindungen ist die Grundlage dafür, dass sich Moleküle und damit chemische Verbindungen bilden können. Chemische Bindungen liegen vor, wenn zwei oder mehrere Atome oder Ionen stark miteinander verbunden sind und dadurch chemische Verbindungen bilden. Dass es überhaupt zur Ausbildung von chemischen Bindungen kommt, beruht darauf, dass es für die betroffenen Atome oder Ionen energetisch günstiger ist, mit geeigneten Bindungspartnern verbunden zu sein, als separat in Form von einzelnen, ungebundenen Teilchen vorzuliegen. Grundlage der Ausbildung von Bindungen sind elektrostatische Wechselwirkungen oder Wechselwirkungen der Elektronen zwischen zwei oder mehreren Atomen. In vielen Fällen spielen beide Arten von Wechselwirkungen eine Rolle.

Zur Beschreibung einer Bindung sind zwei Parameter wichtig, die sich experimentell bestimmen und untersuchen lassen, die Bindungslänge als Maß für den Abstand zweier Atomkerne und die Bindungsenergie, als Maß für die Stärke einer Bindung.

Bei chemischen Bindungen werden verschiedene Arten unterschieden. Bei Verbindungen vom Typ der Salze werden Ionenkristalle durch die auf elektrostatischen Wechselwirkungen beruhenden ionischen Bindungen gebildet. In Metallen liegen metallische Bindungen vor, die sich dadurch auszeichnen, dass die beteiligten Elektronen in einem Gitter, gebildet aus Metallkationen, frei beweglich sind. Dagegen beruht die Bildung von Molekülen und Komplexen auf lokalisierbaren kovalenten Bindungen zwischen Atomen, die auf der Bildung von Elektronenpaaren basieren. Dabei kann man bei den lokalisierbaren Elektronenpaarbindungen zusätzlich unterscheiden zwischen der kovalenten Bindung, bei der beide Atome jeweils ein Elektron zur Bindung beitragen, und der koordinativen Bindung in Komplexen, bei der das eine Elektronenpaar des Liganden mit einem leeren Orbital des Zentralatoms wechselwirkt. In speziellen Fällen können Mehrzentrenbindungen auftreten. Metallische, ionische und kovalente Bindungen sind Idealisierungen der chemischen Bindungen.^[1]

Mitunter werden auch schwache Wechselwirkungen, wie die Van-der-Waals-Wechselwirkungen, Dipol-Wechselwirkungen und Wasserstoffbrückenbindungen zu den chemischen Bindungen gezählt. Jedoch sind diese Bindungen keine stabilen chemischen Bindungen, sondern schwache Anziehungskräfte, die zwischen einzelnen Molekülen wirken.

Für die Beschreibung der Bindungen in Molekülen wurden in der theoretischen Chemie verschiedene Theorien aufgestellt, die jedoch alle nur möglichst exakte Näherungen der tatsächlichen Bindungssituation sind. Zu ihnen zählen die Valenzstruktur- und die Molekülorbitaltheorie.

Bindungen lassen sich durch die Zuführung von Energie, etwa in Form von Wärme oder Licht, spalten. Die dadurch entstehenden einzelnen Atome oder Moleküle haben häufig eine hohe Neigung, sich erneut zu binden. Die Neubindung kann an der vorher gespaltenen Stelle stattfinden, oder sie erfolgt an anderen Atomen oder Molekülen. Dies ist eine der Grundlagen für chemische Reaktionen.

Die Entwicklung von verschiedenen Theorien zur chemischen Bindung ist eng mit der Entwicklung von Theorien und Experimenten zur Gestalt des einzelnen Atoms verbunden. Die ersten konkreten Theorien wurden nach der Entdeckung des Elektrons durch Joseph John Thomson 1897 aufgestellt. In seinem Atommodell stellte Thomson sich vor, dass die chemischen Bindungen auf elektrostatischen Kräften beruhen, die durch den Transfer von einem zum anderen Atom entstehen. Dadurch ergab sich zunächst die Annahme, dass chemische Bindungen immer polar aufgebaut sein müssen.^[2]

Auf Grund der Eigenschaften organischer Verbindungen, die nicht mit polaren Bindungen zu erklären waren, und Versuchen mit Kanalstrahlen wurde bald klar, dass es auch eine unpolare Bindung geben muss. Gilbert Lewis vermutete erstmals 1916, dass die unpolare Bindung auf gepaarten Elektronen beruht. Diese Theorie war auch mit den Atommodellen von Rutherford und Bohr vereinbar, die inzwischen das Thomson'sche Modell abgelöst hatten.^[2]

Mit der Entwicklung der Quantenmechanik und vor allem der Aufstellung der Schrödingergleichung durch Erwin Schrödinger 1926 konnten genauere Theorien der Bindung aufgestellt werden. Die erste quantenmechanische Theorie wurde mit der Valenzstrukturtheorie 1927 durch Walter Heitler und Fritz London entwickelt.^[3] Die ursprüngliche Theorie war zunächst nur für das einfachste Molekül, das H₂⁺-Ion aus zwei Protonen und einem Elektron gültig. Linus Pauling erweiterte die Theorie durch die Einführung des Orbitals und der Hybridisierung umfangreich, so dass die Theorie auf kompliziertere Moleküle angewendet werden konnte.^[2]

Ebenfalls im Jahr 1927 wurde von Friedrich Hund und Robert Mulliken die genauere Molekülorbitaltheorie aufgestellt. Auch diese war zunächst nur für einfache Moleküle anwendbar, wurde jedoch nach und nach erweitert, beispielsweise 1930 von Erich Hückel durch eine genauere Erklärung von Mehrfachbindungen mit der Erklärung der π-Bindung.^[3]

Nachdem die grundlegenden quantenmechanischen Theorien aufgestellt waren, versuchten verschiedene Forscher, über diese Theorien beobachtete Phänomene der organischen oder anorganischen Chemie zu erklären. Wichtige Beispiele sind die Ligandenfeldtheorie für Komplexe, die 1951 von Hermann Hartmann und F. E. Ilse veröffentlicht wurde und die 1968 von Robert B. Woodward und Roald Hoffmann aufgestellten Woodward-Hoffmann-Regeln, mit denen eine bestimmte Art organischer Reaktionen, die pericyclischen Reaktionen auf Basis der Molekülorbitaltheorie verstanden werden konnte.^[4]

Mit der Entwicklung des Computers ab etwa 1950 wurden auch kompliziertere theoretische Berechnungen zur chemischen Bindung möglich. Eine wichtige Entwicklung dafür waren unter anderem die der Roothaan-Hall-Gleichungen durch Clemens C. J. Roothaan und George G. Hall im Jahr 1951, die in der Hartree-Fock-Methode wichtig sind.^[4] Ab 1964 wurde von Walter Kohn schließlich mit der Dichtefunktionaltheorie eine weitere Möglichkeit zur theoretischen Berechnung der chemischen Bindung entwickelt. Er erhielt dafür den Chemie-Nobelpreis 1998.^[5]

(c) Goran tek-en, CC BY-SA 4.0

Die ionische Bindung ist eine ungerichtete Bindung mit großer Reichweite, die in alle Raumrichtungen gleich stark wirkt. Sie ist die vorherrschende Bindungsart bei Salzen, also bei Verbindungen gebildet aus Metall-Kationen und Nichtmetall-Anionen, die periodisch in sog. Ionengittern angeordnet sind. Bei der Reaktion von Metallen mit Nichtmetallen kann es durch Elektronegativitätsdifferenzen der beteiligten Elemente zu einer Übertragung von Valenzelektronen des Metalls auf das Nichtmetall und damit zur Bildung von elektrisch geladenen Atomen kommen, den sogenannten Ionen. Je größer die jeweilige Elektronegativitätsdifferenz ist, desto ionischer ist die neu gebildete Bindung. Jedoch sind bei allen ionischen Bindungen auch kovalente Anteile an der Bindung vorhanden. Bei niedrigen Differenzen kommt es nur zu eingeschränkten Übertragungen und es ist für die Beschreibung der neuen Bindung nötig, beide Anteile zu berücksichtigen.

Für die Bindungen in den gebildeten Ionenkristallen sind überwiegend die elektrostatische Wechselwirkungen zwischen den unterschiedlich geladenen Kationen und Anionen verantwortlich. Der energetische Zustand im jeweiligen Ionenkristall lässt sich theoretisch gut mit der Gitterenergie beschreiben. In die Berechnung der Gitterenergie werden vor allem die anziehenden und abstoßenden Kräfte zwischen den Ionen, und die Abstoßung der sich durchdringenden Elektronenhüllen einbezogen und das Coulomb-Gesetz berücksichtigt. Die Art des Gitters wird über die Madelung-Konstante einbezogen.

Ionische Bindungen sind starke Bindungen und haben deshalb hohe Schmelztemperaturen vieler ionisch aufgebauter Substanzen zur Folge. Typische Werte für die Gitterenergie von zwei aus Ionen gebildeten Ionengitter liegen für Natriumchlorid bei 787 kJ/mol (8,2 eV) und bei 3850 kJ/mol (39,9 eV) für das höher geladene Magnesiumoxid (beide Werte bestimmt über den Born-Haber-Kreisprozess).^[6]

Wichtig für die Bildung von Natriumchlorid aus den Elementen Natrium und Chlor ist die Erkenntnis, dass für die Abspaltung eines Elektrons aus Natrium mit 495 kJ/mol (Ionisierungsenergie) mehr Energie erforderlich ist, als mit 349 kJ/mol (Elektronenaffinität) bei der Aufnahme des Elektrons durch Chlor geliefert wird. Dass die Reaktion trotzdem rasant unter Energiegewinn abläuft, liegt damit allein an der Bildung des Ionengitters, die mit 788 kJ/mol (Gitterenergie) formal zur treibenden Kraft der Reaktion wird.^[7]

Da die ionische Bindung ungerichtet ist, ist sie jedoch nicht stärker als viele kovalente Bindungen, die nur innerhalb eines Moleküls und nicht zwischen den Molekülen eines Stoffes wirken. Die elektrostatische Natur der Ionenbindung bedingt die Sprödigkeit vieler Ionenkristalle, da bei Verschiebungen zwischen den Ionen leicht gleichgeladene Ionen aneinandergrenzen, die sich abstoßen und so den Kristall auseinandersprengen.

Die kovalente Bindung ist diejenige Bindung, die in Nichtmetallverbindungen sowie Komplexen vorherrscht. Sie ist im Gegensatz zur ionischen Bindung gerichtet und an eine bestimmte Stelle zwischen zwei einzelnen Atomen gebunden. Ausnahmen sind die Mehrzentrenbindungen, bei denen drei oder mehr Atome kovalent gebunden sind, und die delokalisierten π-Bindungen, bei denen mehrere Bindungen zu einer einzigen Elektronenwolke verschmolzen sind.

Kovalente Bindungen beruhen normalerweise auf einem so genannten Elektronenpaar, das aus den Valenzelektronen der beteiligten Atome gebildet wird. Um eine kovalente Bindung in einer chemischen Formel darzustellen, wird diese in der Lewis-Formel durch einen Strich, manchmal auch durch zwei Punkte symbolisiert. Theoretisch wird die kovalente Bindung mit zwei verschiedenen Theorien, der Molekülorbital- und der Valenzstrukturtheorie, erklärt. Ältere Theorien für Komplexe sind die Kristallfeld- und Ligandenfeldtheorie, jedoch lassen sich die Bindungsverhältnisse in Komplexverbindungen genauer durch die Molekülorbitaltheorie vorhersagen.^[8]

Die Stärke einer kovalenten Bindung hängt von der Art der Bindung, den beteiligten Atomen und der Bindungslänge ab. Die stärksten kovalenten Bindungen sind die kurzen Dreifachbindungen von Elementen der zweiten Periode wie Kohlenstoff, Stickstoff oder Sauerstoff, so beträgt die Dissoziationsenergie einer Stickstoff-Stickstoff-Dreifachbindung 941,7 kJ/mol (9,8 eV).^[9] Bindungsenergien für Einfachbindungen liegen in der Regel zwischen 150 und 500 kJ/mol (etwa 1,5–5 eV), bei Doppelbindungen liegen Bindungsenergien typischerweise bei 500–800 kJ/mol (5–8 eV) für die zweite Periode (O-O-Doppelbindung: 493,6 kJ/mol, C-O-Doppelbindung: 798,9 kJ/mol), für die schwächeren Doppelbindungen der höheren Perioden darunter.^[9]

Die Valenzstrukturtheorie versucht, eine Bindung quantenmechanisch zu beschreiben. Sie ist zunächst für das Wasserstoffmolekül mit zwei Protonen und zwei Elektronen mit unterschiedlichem Spin aufgestellt worden und kann durch Ergänzungen und Vereinfachungen auch für kompliziertere Moleküle angewendet werden. Für genaue Berechnungen müssen zunächst die Wellenfunktionen der beteiligten Elektronen aufgestellt werden. Diese unterscheiden sich je nach Orbital, in dem sich das Elektron befindet. Im Gegensatz zur Molekülorbitaltheorie werden die Bindungen in der Regel einzeln und nicht das Molekül als Ganzes betrachtet.

In der einfachsten Näherung wird die Gesamtwellenfunktion Ψ des H₂-Moleküls als Produkt der beiden Wellenfunktionen der beiden Elektronen gesehen.

${\displaystyle \Psi =\Psi _{\mathrm {A(1)} }\cdot \Psi _{\mathrm {B(2)} }}$

A: 1. Atom, B: 2. Atom, 1: 1. Elektron, 2: 2. Elektron

Dies berücksichtigt noch keine Beeinflussungen der Elektronen untereinander und gilt somit exakt nur für zwei isolierte Wasserstoffatome. Für genauere Ergebnisse für gebundene Atome muss vor allem die Austauschenergie mit einbezogen werden, die dadurch zustande kommt, dass die Elektronen nicht an einem Atom lokalisiert sind, sondern an beiden eine Aufenthaltswahrscheinlichkeit besitzen. Die Wellenfunktion wird dann als

${\displaystyle \Psi =\Psi _{\mathrm {A(1)} }\cdot \Psi _{\mathrm {B(2)} }+\Psi _{\mathrm {A(2)} }\cdot \Psi _{\mathrm {B(1)} }}$

geschrieben. Mit Verfeinerungen, etwa der Einbeziehung der Abschirmung, kann eine weitere Annäherung der Theorie an den experimentellen Wert erreicht werden.

Ein wichtiges Konzept, mit dem man die Valenzstrukturtheorie auf kompliziertere Moleküle ausweiten kann, ist die Hybridisierung. Dazu werden aus unterschiedlichen Orbitalarten Hybridorbitale gebildet. Am bekanntesten sind die aus einem s- und drei p-Orbitalen gebildeten sp³-Hybridorbitale, die vor allem zur Erklärung der Bindungssituation in Kohlenstoffatomen verwendet werden. Dabei werden aus den im Kohlenstoffatom vorhandenen drei p-Orbitalen und dem 2s-Orbital vier gleiche sp³-Hybridorbitale gebildet, die tetraedrisch angeordnet sind und Bindungen zu benachbarten Atomen bilden. Es ist auch möglich, dass nur eines oder zwei der p-Orbitale an der Hybridisierung beteiligt sind. Dann bilden sich sp- oder sp²-Hybridorbitale. Das Konzept der Hybridisierung ist jedoch nicht dazu geeignet, Vorhersagen für Verbindungen mit bisher unbekanntem räumlichen Aufbau zu treffen, da sie entwickelt wurde, indem, von der räumlichen Struktur ausgehend, passende Orbitale so gemischt wurden, dass sie die reale Struktur beschreiben. Daher kann ausschließlich von der räumlichen Struktur auf die Hybridorbitale geschlossen werden, jedoch nicht umgekehrt.

Je nachdem, welche Orbitale beteiligt sind, werden verschiedene Bindungsarten unterschieden. Ist eine Bindung rotationssymmetrisch um die Kern-Kern-Verbindungsachse, so handelt es sich um eine σ-Bindung. Diese besteht meist nur aus s- und/oder sp-Hybridorbitalen. In seltenen Fällen wird eine σ-Bindung von zwei d_z²-Orbitalen gebildet. σ-Bindungen liegen direkt auf der Verbindungsachse zwischen den Atomen und besitzen keine Knotenebene. p-Orbitale bilden π-Bindungen, die oberhalb und unterhalb der Kernverbindungsachse liegen und eine Knotenebene besitzen. Sie sind für die Beschreibung von Doppel- und Dreifachbindungen wichtig. Sehr selten kommen auch Vier- oder Fünffachbindungen vor, die neben σ- und π-Bindungen aus d-Orbitalen gebildete δ-Bindungen aufweisen.

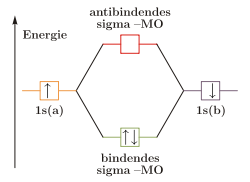
Wie die Valenzstrukturtheorie ist die Molekülorbitaltheorie eine auf quantenmechanischen Grundlagen beruhende Theorie. Bei diesem Ansatz werden jedoch die Atome nicht getrennt betrachtet, sondern es wird zunächst aus den einzelnen Atomorbitalen ein Molekülorbital gebildet, in das die Elektronen gemäß der Hundschen Regel und dem Pauli-Prinzip eingeordnet werden.

Molekülorbitale werden durch Linearkombination der beteiligten Atomorbitale gebildet („LCAO-Methode“). Durch die Linearkombination werden immer zwei Molekülorbitale, ein bindendes und ein antibindendes, gebildet, die der Addition beziehungsweise Subtraktion der Wellenfunktionen der beiden Atomorbitale entsprechen.

${\displaystyle \mathrm {\ \Psi _{b}=\Psi _{A}+\Psi _{B}} }$

Bildung des bindenden Orbitals

${\displaystyle \mathrm {\ \Psi _{a}=\Psi _{A}-\Psi _{B}} }$

Bildung des antibindenden Orbitals

• 
  Wellenfunktion eines bindenden s-Orbitals
• 
  Wellenfunktion eines antibindenden s-Orbitals

Im bindenden Molekülorbital ist das Überlappungsintegral positiv und dadurch die Elektronendichte zwischen den Atomen erhöht. Durch die erhöhte Elektronendichte sind die Kerne voneinander besser abgeschirmt, was energetisch günstig ist. Es bildet sich daher eine Bindung aus. Im antibindenden ist das Überlappungsintegral dagegen negativ, es kommt zu einer Knotenebene und einer geringeren Elektronendichte zwischen den Kernen. Da dies energetisch ungünstig ist, kann sich keine Bindung ausbilden.

Der energetisch günstigste Abstand zweier Atome und der Energiegewinn bei der Bindung im Vergleich zum ungebundenen Zustand, der die Stärke der Bindung bedingt, können bei einfachen Systemen wie dem H₂ und dem H₂⁺-Molekül nach der LCAO-Näherung (Linear Combination of Atomic Orbitals) näherungsweise über das Potential berechnet werden. Dazu müssen verschiedene anziehende und abstoßende Faktoren berücksichtigt werden. Dies ist zum einen die gegenseitige Abstoßung der gleichgeladenen Kerne und bei Mehrelektronensystemen wie dem H₂-Molekül auch der Elektronen untereinander. Dagegen wirken die Wechselwirkungen zwischen den positiv geladenen Kernen und den negativ geladenen Elektronen anziehend und bedingen so einen Energiegewinn. Nur wenn die aus diesen Faktoren berechnete Potentialkurve ein Minimum aufweist, kann eine Bindung stabil sein.^[10]

Werden in einem Molekülorbital die bindenden und antibindenden Orbitale mit Elektronen besetzt, lässt sich die Bindungsordnung bestimmen. Dazu wird die Anzahl an Elektronen in den antibindenden Molekülorbitalen von der in den bindenden Molekülorbitalen abgezogen. Ist die theoretische Bindungsordnung, wie beim He₂-Molekül, null, ist das Molekül instabil, das Molekül wird nur durch die schwachen Van-der-Waals-Wechselwirkungen zusammengehalten.^[11]

• 
  HOMO (bindend) der π-Bindung bei Ethen
• 
  LUMO (antibindend) der π-Bindung bei Ethen

Die Kristallfeldtheorie und ihre Erweiterung, die Ligandenfeldtheorie, versuchen die Bindungssituation in Komplexen, also Verbindungen mit einem Metallzentrum, in der Regel einem Übergangsmetall, und darumliegenden Liganden, Nichtmetallatomen oder kleinen Molekülen wie etwa Chlorid oder Wasser, zu erklären.

Im Gegensatz zu den meisten Molekülen sind bei Komplexen die d-Orbitale des Metallatoms entscheidend an der Bindung beteiligt. Diese werden in ihrer Energie durch elektrostatische Wechselwirkungen mit den Liganden beeinflusst. Je nach Geometrie des Komplexes wird die Energie der einzelnen Orbitale unterschiedlich stark erhöht. Daher kommt es zur Aufhebung der Entartung der verschiedenen Orbitale und zu einer für jede Komplexgeometrie typischen Aufspaltung der Orbitalenergien. Die Stärke der Aufspaltung hängt von der Art des Zentralions, seiner Oxidationsstufe, der Geometrie des Komplexes und Art der Liganden ab. Deren unterschiedliche Fähigkeit zur Energieaufspaltung ist in der spektrochemischen Reihe festgelegt.

Mit der Kristallfeldtheorie sind viele Eigenschaften von Komplexen gut erklärbar. So lassen sich die Farbe, die magnetischen Eigenschaften und die Stabilität von Komplexen damit vorhersagen. Die Theorie ist allerdings begrenzt, so lässt sich etwa die besondere Stärke von Kohlenstoffmonoxid als Ligand und der nephelauxetische Effekt nicht über die Kristallfeldtheorie erklären. Genauere Ergebnisse liefert dafür die Molekülorbitaltheorie, bei der nicht nur die d-Orbitale des Zentralatoms, sondern alle beteiligten Orbitale in die Berechnungen mit einbezogen werden.^[8]

Die Bindigkeit, also die Anzahl an Bindungen, die ein Atom eingehen kann, wird von den Orbitalen bestimmt. Es ist gemäß der Edelgasregel günstig, vollbesetzte oder leere Orbitale zu bilden. Zudem bilden die größeren d- und f-Orbitale energetisch günstig halbbesetzte Orbitale (d⁵ und f⁷-Konfiguration) aus, bei denen alle Orbitale von einem Elektron mit parallelem Spin besetzt sind. Daher nimmt ein Atom in der Regel so viele Elektronen von benachbarten Atomen auf und bildet Bindungen aus, bis es die Edelgaskonfiguration erreicht hat. Da die maximale Anzahl an Valenzelektronen, die ein Atom der zweiten Periode erreichen kann, acht beträgt, wird häufig von der Oktettregel gesprochen. So besitzt beispielsweise Sauerstoff selbst sechs Valenzelektronen und kann noch zwei weitere aufnehmen. Dementsprechend bildet er auch in der Regel zwei Bindungen zu anderen Atomen aus; das stabile Oxid-Ion ist durch die Aufnahme zweier zusätzlicher Elektronen zweifach negativ geladen.

Bei der metallischen Bindung liegen im Gegensatz zur ionischen oder kovalenten Bindung frei bewegliche Elektronen vor, die nicht an ein bestimmtes Atom gebunden sind. Ein einfaches Modell ist das des Elektronengases, bei dem die Valenzelektronen ein negativ geladenes „Gas“ bilden, das die positiv geladenen „Atomrümpfe“ eines Metallgitters vollständig umgibt und für den Ladungsausgleich sorgt. Der Energiegewinn bei Ausbildung einer metallischen Bindung resultiert vorwiegend aus der starken Reduzierung der kinetischen Energie der Teilchen im Elektronengas.^[12] Ein stabiles metallisches Gitter ergibt sich durch Überlagerung und Summierung der Abstoßung zwischen den Atomrümpfen sowie der Anziehung zwischen dem Elektronengas und den positiv geladenen Metallkationen in einem Gleichgewichtsabstand der Atomrümpfe. Im festen Zustand sind diese in der dichtest-möglichen Packung angeordnet; etwa 60 % aller Metalle kristallisieren in der hexagonal oder kubisch dichtesten Kugelpackung.^[13]

Ein genaueres Modell der metallischen Bindung ist das aus der Molekülorbitaltheorie ableitbare Bändermodell, das vorwiegend zur Beschreibung von Metallen verwendet wird, jedoch auch Eigenschaften von Salzen und Halbleitern erklären kann. Dabei werden aus den Valenzorbitalen bindende und antibindende Molekülorbitale gebildet. Auf Grund des Pauli-Prinzips besitzt jedes Atomorbital eine geringfügig andere Energie, so dass die Molekülorbitale im Metall breite Bänder bilden. Die aus verschiedenen Molekülorbitalen gebildeten Bänder können sich überlappen oder es bilden sich Bandlücken zwischen ihnen.

Die Elektronen füllen die Bänder bis zu einem bestimmten Niveau, dem Fermi-Niveau. Liegt dieses innerhalb eines Bandes, so braucht es für den Übergang eines Elektrons von den besetzten in die unbesetzten Niveaus fast keine Energie und es liegt ein Metall mit der typischen Leitfähigkeit vor. Liegt das Fermi-Niveau gerade an einer Bandlücke, so ist dieser einfache Übergang eines Elektrons in das Leitungsband nicht mehr möglich, der Stoff ist nicht leitend. Bei kleinen Bandlücken ist es aber möglich, dass durch äußere Zufuhr an Energie, etwa in Form von Wärme, die Elektronen die Lücke trotzdem überwinden können und ein derartiger Stoff leitend wird. Diese Stoffe werden daher Halbleiter genannt.

Schwache Bindungen werden manchmal auch zu den Bindungen gezählt, sind jedoch keine eigentlichen Bindungen innerhalb von Molekülen, sondern Wechselwirkungen, die zwischen verschiedenen Molekülen wirken und schon mit geringer Energiezufuhr gebrochen werden können. In der Regel reicht die Bewegungsenergie der Atome und Moleküle aus, um eine solche Bindung schon nach sehr kurzer Zeit wieder zu brechen.

Die stärkste der schwachen Bindungen ist die Wasserstoffbrückenbindung. Diese bildet sich zwischen an Stickstoff, Sauerstoff oder Fluor gebundenen und durch die große Elektronegativitätsdifferenz stark positiv teilgeladenen Wasserstoffatomen und freien Elektronenpaaren dieser Elemente aus. Die bekannteste Verbindung, die Wasserstoffbrücken ausbildet, ist Wasser. Aber auch Ammoniak, Fluorwasserstoff und andere Verbindungen, die N-H- oder O-H-Bindungen besitzen, wie beispielsweise Aminosäuren oder DNA, sind dazu in der Lage. Auf Grund ihrer Stärke beeinflusst die Wasserstoffbrückenbindung die Eigenschaften eines Stoffes stark. Ihre Wirkung zwischen Wassermolekülen ist unter anderem für den ungewöhnlich hohen Schmelzpunkt des Wassers verantwortlich.

Deutlich schwächer sind die Van-der-Waals-Wechselwirkungen, unter denen verschiedene Phänomene, etwa die London-Kräfte und Dipol-Dipol-Wechselwirkungen zusammengefasst werden. Diese Kräfte lassen sich mit spontanen und induzierten Dipolen bzw. dauerhaften Dipolen erklären, die zwischen den Molekülen der jeweiligen Stoffe wirken. Deshalb können auch Substanzen, die unpolare Moleküle enthalten, bei Standardbedingungen als Flüssigkeit oder Feststoff vorliegen.

Für die Untersuchung von Bindungen sind neben der Messung von Stoffeigenschaften, aus denen auf Eigenschaften der Bindung geschlossen werden kann, theoretische Berechnungen von großer Bedeutung. Dabei wird versucht, die für ein gegebenes System aufgestellte Schrödingergleichung zu lösen. Da diese Berechnungen auch für einfache molekulare Systeme (zumindest ohne drastische Näherungen) nicht in geschlossener Form durchführbar und numerisch in der Regel aufwendig sind, werden sie im Allgemeinen mit Hilfe entsprechender Computerprogramme durchgeführt. Häufig werden die sogenannten ab-initio-Verfahren genutzt, die ohne empirische Parameter auskommen. Ein auch für kompliziertere Systeme genutztes Verfahren ist das Hartree-Fock-Verfahren. Das Ziel ist hierbei, aus den Wellenfunktionen der einzelnen Elektronen die Gesamtwellenfunktion der Elektronen des Systems, also etwa eines Moleküls zu berechnen. Dazu wird das Produkt der einzelnen Orbitale in Form der Slaterdeterminante aufgestellt. Gemäß dem Rayleigh-Ritz-Prinzip ist die über die Slaterdeterminante berechnete Energie immer größer oder gleich der tatsächlichen Energie des Systems. Durch eine Variation der Orbitale lässt sich dann die minimale Energie berechnen.^[14] Auf das für quantitative Zwecke häufig nicht hinreichend genaue Hartree-Fock-Verfahren baut eine Reihe so genannter Post-Hartree-Fock-Verfahren auf.

Eine weitere Theorie, mit der Bindungen untersucht werden können, ist die Dichtefunktionaltheorie. Sie rechnet im Gegensatz zum Hartree-Fock-Verfahren nicht mit den Wellenfunktionen der einzelnen Elektronen, sondern mit der Elektronendichte.^[15]

Die Art und Stärke von chemischen Bindungen lassen sich nicht direkt beobachten, sondern müssen aus Eigenschaften eines Stoffes abgeleitet werden. Stoffeigenschaften, die Hinweise auf die Natur einer Bindung geben, sind beispielsweise der Schmelzpunkt, Glanz, optische Eigenschaften oder die Duktilität einer Verbindung. So sind ein hoher Schmelzpunkt, Sprödigkeit oder optische Transparenz Hinweise auf eine ionische Bindung, während metallischer Glanz, Opazität und Duktilität auf metallische Bindungen hindeuten. Kovalent aufgebaute Verbindungen besitzen dagegen häufig einen niedrigen Schmelzpunkt und liegen dementsprechend vielfach in flüssigem oder gasförmigem Aggregatzustand vor. Diese Eigenschaften sind jedoch nicht eindeutig, so besitzt Diamant Eigenschaften wie optische Transparenz und einen hohen Schmelzpunkt, die auf ionische Bindungen hindeuten, ist jedoch vollständig aus kovalenten Bindungen aufgebaut.

Für die genauere Untersuchung der Bindung müssen die Bindungslänge und die Bindungsenergie sowie die Geometrie einer Verbindung bestimmt werden. Untersuchungsmethoden zur Bestimmung dieser Eigenschaften unterscheiden sich je nach Verbindungsart und Aggregatzustand. Die wichtigsten Methoden zur Bestimmung der Bindungslänge in Festkörpern sind die Röntgen- und Neutronenbeugung. Über sie können die Positionen der einzelnen Atome im Kristall und damit die Abstände und Bindungswinkel untereinander ermittelt werden. Diese Methoden lassen sich jedoch nur bei Festkörpern, nicht bei Flüssigkeiten oder Gasen anwenden. Bei einfach aufgebauten gasförmigen Molekülen lässt sich aus Rotationsspektren über das Trägheitsmoment eine Bindungslänge berechnen. Da auch die Geometrie Einfluss auf das Trägheitsmoment besitzt, kann auch sie aus den Rotationsspektren abgeleitet werden.

Die exakte Bindungsenergie lässt sich experimentell nicht bestimmen. Näherungsweise wird sie aus den Dissoziationsenthalpien möglichst einfacher Moleküle ermittelt, für genaue theoretische Werte müssen zusätzliche Faktoren wie die Nullpunktenergie, Rotationsenergien oder die Volumenarbeit beachtet werden.^[16] Für die Ermittlung der Dissoziationsenthalpie kann dabei die Schwingungsspektroskopie eingesetzt werden. Ebenso wie die Bindungsenergie einer kovalenten Bindung kann auch die Gitterenergie einer ionischen Verbindung nicht direkt gemessen werden. Sie wird indirekt über den Born-Haber-Kreisprozess berechnet.

Informationen über Bindungen lassen sich auch aus kinetischen Untersuchungen wie Stoß- und Streuexperimenten im Molekularstrahl gewinnen. Über diese lassen sich Potentialflächen von Molekülen und damit Stärke einer Bindung und der günstigste Abstand zweier Atome bestimmen.^[17]

• Eintrag zu Chemische Bindung. In: Römpp Online. Georg Thieme Verlag, abgerufen am 26. Mai 2014.
• James E. Huheey, Ellen A. Keiter, Richard L. Keiter: Anorganische Chemie. 3. Auflage. de Gruyter, Berlin 2003, ISBN 3-11-017903-2.
• A. F. Holleman, E. Wiberg, N. Wiberg: Lehrbuch der Anorganischen Chemie. 102. Auflage. Walter de Gruyter, Berlin 2007, ISBN 978-3-11-017770-1.
• Werner Kutzelnigg: Einführung in die Theoretische Chemie, Teil II: Die chemische Bindung. Wiley-VCH, Weinheim 2002, ISBN 3-527-30609-9.
• Joachim Reinhold: Quantentheorie der Moleküle. 3. Auflage. Teubner, Wiesbaden 2006, ISBN 3-8351-0037-8.
• Linus Pauling: Die Natur der chemischen Bindung. 2. Nachdruck der aus dem Englischen übersetzten 3. Auflage von 1960, Wiley-VCH, Weinheim 1988, ISBN 3-527-25217-7.

• Chemische Bindungen. In: Die Chemieseite. Christoph Tornau, abgerufen am 9. Juni 2009 (umfangreiche Erklärungen zur chemischen Bindung).  (private Seite)
• Chemische Bindungsarten mit Erklärungen und bildlichen Darstellungen. (private Seite)
• Videotutorials zu chemischen Bindungen – hier werden in verschiedensten Videos sowohl die wesentlichen Bindungsarten als auch intermolekulare Wechselwirkungen erklärt (private Seite)

1. ↑ Theodore L. Brown, H. Eugene LeMay, Bruce E. Bursten: Chemie. Die zentrale Wissenschaft. Pearson Studium, 2007, ISBN 978-3-8273-7191-1, S. 353. 
2. ↑ ^{a b c} William H. Brock: Viewegs Geschichte der Chemie. Vieweg, Braunschweig 1997, ISBN 3-540-67033-5, S. 292–319.
3. ↑ ^{a b} Friedrich Hund: Frühgeschichte der quantenmechanischen Behandlung der chemischen Bindung. In: Angewandte Chemie 89, 1977, S. 89–94 (doi:10.1002/ange.19770890206).
4. ↑ ^{a b} Werner Kutzelnigg: Einführung in die Theoretische Chemie. Teil II: Die chemische Bindung. Wiley-VCH, Weinheim 2002, ISBN 3-527-30609-9, S. 4–7.
5. ↑ Walter Kohn: Electronic structure of matter – wave functions and densityfunctionals. Nobelpreis-Vortrag, 1999 (PDF).
6. ↑ Peter W. Atkins, Julio de Paula: Physikalische Chemie. 4. Auflage. Wiley-VCH, Weinheim 2006, ISBN 3-527-31546-2, S. 1129.
7. ↑ Theodore L. Brown, H. Eugene LeMay, Bruce E. Bursten: Chemie. Die zentrale Wissenschaft. Pearson Studium, 2007, ISBN 978-3-8273-7191-1, S. 356, 321, 316. 
8. ↑ ^{a b} James E. Huheey, Ellen A. Keiter, Richard L. Keiter: Anorganische Chemie. 3. Auflage. de Gruyter, Berlin 2003, ISBN 3-11-017903-2, S. 480.
9. ↑ ^{a b} James E. Huheey, Ellen A. Keiter, Richard L. Keiter: Anorganische Chemie. 3. Auflage. de Gruyter, Berlin 2003, ISBN 3-11-017903-2, S. 1164–1167.
10. ↑ Werner Kutzelnigg: Einführung in die Theoretische Chemie, Teil II: Die chemische Bindung. Wiley-VCH, Weinheim 2002, ISBN 3-527-30609-9, S. 63 ff.
11. ↑ R. E. Grisenti, W. Schöllkopf, J. P. Toennies, G. C. Hegerfeldt, T. Köhler, M. Stoll: Determination of the Bond Length and Binding Energy of the Helium Dimer by Diffraction from a Transmission Grating. In: Phys. Rev. Lett. 85, Nr. 11, 2000, S. 2284–2287 (doi:10.1103/PhysRevLett.85.2284).
12. ↑ Siegfried Hunklinger: Festkörperphysik. Oldenbourg Wissenschaftsverlag, 2007, ISBN 978-3-486-57562-0, S. 25.
13. ↑ Hans P. Latscha, Helmut A. Klein, Klaus Gulbins: Chemie für Laboranten und Chemotechniker. 2. Allgemeine und anorganische Chemie. 2. Auflage. Springer, 1992, ISBN 3-540-55164-6, S. 61–63.
14. ↑ Eintrag zu Hartree-Fock-Verfahren. In: Römpp Online. Georg Thieme Verlag, abgerufen am 3. Januar 2015.
15. ↑ Eintrag zu Dichtefunktionaltheorie. In: Römpp Online. Georg Thieme Verlag, abgerufen am 3. Januar 2015.
16. ↑ James E. Huheey, Ellen A. Keiter, Richard L. Keiter: Anorganische Chemie. 3. Auflage. de Gruyter, Berlin 2003, ISBN 3-11-017903-2, S. 1155–1159.
17. ↑ Dudley R. Herschbach: Molekulare Dynamik chemischer Elementarreaktionen (Nobel-Vortrag). In: Angewandte Chemie 99, Nr. 12, 1986, S. 1251–1275 (doi:10.1002/ange.19870991206).