Binomialverteilung
| Binomialverteilung | |
Wahrscheinlichkeitsfunktion  Drei Wahrscheinlichkeitsfunktionen für Binomialverteilungen mit den Parametern , und | |
Verteilungsfunktion Drei Verteilungsfunktionen für Binomialverteilungen mit den Parametern , und [Das N in der Legende der drei Verteilungsfunktionen entspricht dem der Dichtefunktionen.] | |
| Parameter | , |
|---|---|
| Träger | |
| Wahrscheinlichkeitsfunktion | |
| Verteilungsfunktion | |
| Erwartungswert | |
| Median | i. A. keine geschlossene Formel, siehe unten |
| Modus | oder |
| Varianz | |
| Schiefe | |
| Wölbung | |
| Entropie | |
| Momenterzeugende Funktion | |
| Charakteristische Funktion | |

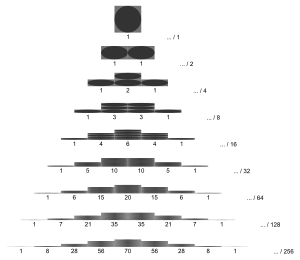
mit und wie im Pascalschen Dreieck
Die Wahrscheinlichkeit, dass eine Kugel in einem Galtonbrett mit acht Ebenen () ins mittlere Fach fällt (), ist .
Die Binomialverteilung ist eine der wichtigsten diskreten Wahrscheinlichkeitsverteilungen.
Sie beschreibt die Anzahl der Erfolge in einer Serie von gleichartigen und unabhängigen Versuchen, die jeweils genau zwei mögliche Ergebnisse haben („Erfolg“ oder „Misserfolg“). Solche Versuchsserien werden auch Bernoulli-Prozesse genannt. Im Urnenmodell wird ein solcher Versuch als Ziehen mit Zurücklegen bezeichnet.
Ist die Erfolgswahrscheinlichkeit bei einem Versuch und die Anzahl der Versuche, dann bezeichnet man mit (auch [1], , [2] oder [3]) die Wahrscheinlichkeit, genau Erfolge zu erzielen (siehe Abschnitt Definition).
Die Binomialverteilung und der Bernoulli-Versuch können mit Hilfe des Galtonbretts veranschaulicht werden. Dabei handelt es sich um eine mechanische Apparatur, in die man Kugeln wirft. Diese fallen dann zufällig in eines von mehreren Fächern, wobei die Aufteilung der Binomialverteilung entspricht. Je nach Konstruktion sind unterschiedliche Parameter und möglich.
Obwohl die Binomialverteilung bereits lange vorher bekannt war, wurde der Begriff zum ersten Mal 1911 in einem Buch von George Udny Yule verwendet.[4]
Definition
Wahrscheinlichkeitsfunktion, Verteilungsfunktion, Eigenschaften
Die diskrete Wahrscheinlichkeitsverteilung mit der Wahrscheinlichkeitsfunktion
heißt die Binomialverteilung zu den Parametern (Anzahl der Versuche) und (der Erfolgs- oder Trefferwahrscheinlichkeit). Bei dieser Formel wird die Konvention angewendet (siehe dazu null hoch null). ist der Binomialkoeffizient.
Eine Zufallsvariable, deren Wahrscheinlichkeitsverteilung eine Binomialverteilung ist, heißt binomialverteilt. Die Binomialverteilung mit den Parametern und wird mit oder bezeichnet. Wenn eine Zufallsvariable die Binomialverteilung besitzt, so wird dies notiert.
Die obige Formel kann so verstanden werden: Wir brauchen bei insgesamt Versuchen genau Erfolge der Wahrscheinlichkeit und haben demzufolge genau Fehlschläge der Wahrscheinlichkeit . Allerdings kann jeder der Erfolge bei jedem der Versuche auftreten, sodass wir noch mit der Anzahl der -elementigen Teilmengen einer -elementigen Menge multiplizieren müssen. Denn genau so viele Möglichkeiten gibt es, aus allen Versuchen die erfolgreichen auszuwählen.
Die zur Erfolgswahrscheinlichkeit komplementäre Ausfallwahrscheinlichkeit wird häufig mit abgekürzt.
Wie für eine Wahrscheinlichkeitsverteilung notwendig, müssen sich die Wahrscheinlichkeiten für alle möglichen Werte zu 1 summieren. Dies ergibt sich aus dem binomischen Lehrsatz wie folgt:
Eine mit der Wahrscheinlichkeitsfunktion verteilte Zufallsgröße heißt dementsprechend binomialverteilt mit den Parametern und sowie der Verteilungsfunktion
- ,
wobei die Abrundungsfunktion bezeichnet.
Weitere gebräuchliche Schreibweisen der kumulierten Binomialverteilung sind , [5] und .[6]
Herleitung als Laplace-Wahrscheinlichkeit
Versuchsschema: Eine Urne enthält Bälle, davon sind schwarz und weiß. Die Wahrscheinlichkeit , einen schwarzen Ball zu ziehen, ist also . Es werden nacheinander zufällig Bälle entnommen, ihre Farbe bestimmt und wieder zurückgelegt.
Wir berechnen die Anzahl der Möglichkeiten, in denen man schwarze Bälle findet, und daraus die sogenannte Laplace-Wahrscheinlichkeit („Anzahl der für das Ereignis günstigen Möglichkeiten, geteilt durch die Gesamtanzahl der (gleichwahrscheinlichen) Möglichkeiten“).
Bei jeder der Ziehungen gibt es Möglichkeiten, insgesamt also Möglichkeiten für die Auswahl der Bälle. Damit genau dieser Bälle schwarz sind, müssen genau der Ziehungen einen schwarzen Ball aufweisen. Für jeden schwarzen Ball gibt es Möglichkeiten, und für jeden weißen Ball Möglichkeiten. Die schwarzen Bälle können noch auf mögliche Weisen über die Ziehungen verteilt sein, also gibt es
Fälle, bei denen genau schwarze Bälle ausgewählt worden sind. Die Wahrscheinlichkeit , unter Bällen genau schwarze zu finden, ist also
Beispiele
Spielwürfel
Die Wahrscheinlichkeit, mit einem fairen Spielwürfel eine 6 zu würfeln, beträgt . Die Wahrscheinlichkeit , dass dies nicht der Fall ist, beträgt . Angenommen, man würfelt 10-mal (), dann beträgt die Wahrscheinlichkeit, dass kein einziges Mal eine 6 gewürfelt wird, . Die Wahrscheinlichkeit, dass genau 2-mal eine 6 gewürfelt wird, beträgt . Allgemein wird die Wahrscheinlichkeit, dass man -mal eine solche Zahl würfelt , durch die Binomialverteilung beschrieben.
Häufig wird der durch die Binomialverteilung beschriebene Prozess auch durch ein sogenanntes Urnenmodell illustriert. In einer Urne seien z. B. 6 Kugeln, 1 davon weiß, die anderen schwarz. Man greife nun 10-mal in die Urne, hole eine Kugel heraus, notiere deren Farbe und lege die Kugel wieder zurück. In einer speziellen Deutung dieses Prozesses wird das Ziehen einer weißen Kugel als positives Ereignis mit der Wahrscheinlichkeit verstanden, das Ziehen einer nicht-weißen Kugel als negatives Ereignis. Die Wahrscheinlichkeiten sind genauso verteilt wie im Beispiel mit dem Spielwürfel.
Münzwurf
Eine Münze wird 7-mal geworfen. Wenn die diskrete Zufallsvariable die Anzahl der Würfe zählt, mit denen „Zahl“ geworfen wird, ergibt sich für eine Binomialverteilung mit der Wahrscheinlichkeitsfunktion
Die Werte und ihre Wahrscheinlichkeiten lassen sich in folgender Tabelle zusammenfassen:
Der Erwartungswert der Zufallsvariablen ist
- .
Die Varianz der Zufallsvariablen ist demnach gegeben durch
Mit dem Verschiebungssatz erhält man ebenfalls den gleichen Wert für die Varianz:
- .
Für die Standardabweichung ergibt sich damit:
- .
Eigenschaften
Symmetrie
- Die Binomialverteilung ist in den Spezialfällen , und symmetrisch und ansonsten asymmetrisch.
- Die Wahrscheinlichkeitsfunktion der Binomialverteilung besitzt die Eigenschaft
- .
Erwartungswert
Eine binomialverteilte Zufallsvariable besitzt den Erwartungswert .
Beweis
Den Erwartungswert errechnet man direkt aus der Definition und der Formel für die Einzelwahrscheinlichkeiten zu
Alternativ kann man verwenden, dass eine -verteilte Zufallsvariable als eine Summe von unabhängigen Bernoulli-verteilten Zufallsvariablen mit geschrieben werden kann. Mit der Linearität des Erwartungswertes folgt dann
Alternativ kann man ebenfalls mit Hilfe des binomischen Lehrsatzes folgenden Beweis geben: Differenziert man bei der Gleichung
beide Seiten nach , ergibt sich
- ,
also
- .
Mit und folgt das gewünschte Ergebnis.
Varianz
Eine binomialverteilte Zufallsvariable besitzt die Varianz .
Beweis
Es sei eine -verteilte Zufallsvariable. Die Varianz bestimmt sich direkt aus dem Verschiebungssatz zu
oder alternativ aus der Gleichung von Bienaymé, angewendet auf die Varianz unabhängiger Zufallsvariablen, wenn man berücksichtigt, dass die identisch verteilten Zufallsvariablen der Bernoulli-Verteilung mit genügen, zu
Die zweite Gleichheit gilt, weil die Einzelexperimente unabhängig sind, sodass die Einzelvariablen unkorreliert sind.
Variationskoeffizient
Aus Erwartungswert und Varianz erhält man den Variationskoeffizienten
Schiefe
Die Schiefe ergibt sich zu
Wölbung
Die Wölbung lässt sich ebenfalls geschlossen darstellen als
Damit ist der Exzess
Modus
Der Modus, also der Wert mit der maximalen Wahrscheinlichkeit, ist für gleich und für gleich . Falls eine natürliche Zahl ist, ist ebenfalls ein Modus. Falls der Erwartungswert eine natürliche Zahl ist, ist der Erwartungswert gleich dem Modus.
Beweis
Sei ohne Einschränkung . Wir betrachten den Quotienten
- .
Nun gilt , falls und , falls . Also:
Und nur im Fall hat der Quotient den Wert 1, d. h. .
Median
Es ist nicht möglich, eine allgemeine Formel für den Median der Binomialverteilung anzugeben. Daher sind verschiedene Fälle zu betrachten, die einen geeigneten Median liefern:
- Ist eine natürliche Zahl, dann stimmen Erwartungswert, Median und Modus überein und sind gleich .[7][8]
- Ein Median liegt im Intervall .[9] Hierbei bezeichnen die Abrundungsfunktion und die Aufrundungsfunktion.
- Ein Median kann nicht zu stark vom Erwartungswert abweichen: .[10]
- Der Median ist eindeutig und stimmt mit round überein, wenn entweder oder oder (außer wenn und gerade ist).[9][10]
- Ist und ungerade, so ist jede Zahl im Intervall ein Median der Binomialverteilung mit Parametern und . Ist und gerade, so ist der eindeutige Median.
Kumulanten
Analog zur Bernoulli-Verteilung ist die kumulantenerzeugende Funktion
- .
Damit sind die ersten Kumulanten und es gilt die Rekursionsgleichung
Charakteristische Funktion
Die charakteristische Funktion hat die Form
Wahrscheinlichkeitserzeugende Funktion
Für die wahrscheinlichkeitserzeugende Funktion erhält man
Momenterzeugende Funktion
Die momenterzeugende Funktion der Binomialverteilung lautet
Summe binomialverteilter Zufallsgrößen
Für die Summe zweier unabhängiger binomialverteilter Zufallsgrößen und mit den Parametern , und , erhält man die Einzelwahrscheinlichkeiten durch Anwendung der Vandermondeschen Identität
also wieder eine binomialverteilte Zufallsgröße, jedoch mit den Parametern und . Somit gilt für die Faltung
Die Binomialverteilung ist also reproduktiv für festes bzw. bildet eine Faltungshalbgruppe.
Wenn die Summe bekannt ist, folgt jede der Zufallsvariablen und unter dieser Bedingung einer hypergeometrischen Verteilung. Dazu berechnet man die bedingte Wahrscheinlichkeit:
Dies stellt eine hypergeometrische Verteilung dar.
Allgemein gilt: Wenn die Zufallsvariablen stochastisch unabhängig sind und den Binomialverteilungen genügen, dann ist auch die Summe binomialverteilt, jedoch mit den Parametern und . Addiert man binomialverteilte Zufallsvariablen mit , dann erhält man eine verallgemeinerte Binomialverteilung.
Beziehung zu anderen Verteilungen
Beziehung zur Bernoulli-Verteilung
Ein Spezialfall der Binomialverteilung für ist die Bernoulli-Verteilung. Die Summe von unabhängigen und identischen Bernoulli-verteilten Zufallsgrößen genügt demnach der Binomialverteilung.
Beziehung zur verallgemeinerten Binomialverteilung
Die Binomialverteilung ist ein Spezialfall der verallgemeinerten Binomialverteilung mit für alle . Genauer ist sie für festen Erwartungswert und feste Ordnung diejenige verallgemeinerte Binomialverteilung mit maximaler Entropie.[11]
Übergang zur Normalverteilung
Nach dem Satz von Moivre-Laplace konvergiert die Binomialverteilung im Grenzfall gegen eine Normalverteilung, d. h., die Normalverteilung kann als brauchbare Näherung der Binomialverteilung verwendet werden, wenn der Stichprobenumfang hinreichend groß und der Anteil der gesuchten Ausprägung nicht zu klein ist. Mit dem Galtonbrett kann man die Annäherung an die Normalverteilung experimentell nachempfinden.
Es gilt und Durch Einsetzen in die Verteilungsfunktion der Standardnormalverteilung folgt
Wie zu sehen, ist das Ergebnis damit nichts anderes als der Funktionswert der Normalverteilung für , sowie (den man sich anschaulich auch als Flächeninhalt des -ten Streifens des Histogramms der standardisierten Binomialverteilung mit als dessen Breite sowie als dessen Höhe vorstellen kann).[12] Die Annäherung der Binomialverteilung an die Normalverteilung wird bei der Normal-Approximation genutzt, um schnell die Wahrscheinlichkeit vieler Stufen der Binomialverteilung zu bestimmen, zumal dann, wenn für diese keine Tabellenwerte (mehr) vorliegen.
Übergang zur Poisson-Verteilung
Eine asymptotisch asymmetrische Binomialverteilung, deren Erwartungswert für und gegen eine Konstante konvergiert, kann man durch die Poisson-Verteilung annähern. Der Wert ist dann für alle in der Grenzwertbildung betrachteten Binomialverteilungen wie auch für die resultierende Poisson-Verteilung der Erwartungswert. Diese Annäherung wird auch als Poisson-Approximation, Poissonscher Grenzwertsatz oder als das Gesetz seltener Ereignisse bezeichnet.
Eine Faustregel besagt, dass diese Näherung brauchbar ist, wenn und .
Die Poisson-Verteilung ist also die Grenzverteilung der Binomialverteilung für große und kleine , es handelt sich hierbei um Konvergenz in Verteilung.
Beziehung zur geometrischen Verteilung
Die Zahl der Misserfolge bis zum erstmaligen Eintritt eines Erfolgs wird durch die geometrische Verteilung beschrieben.
Beziehung zur negativen Binomialverteilung
Die negative Binomialverteilung hingegen beschreibt die Wahrscheinlichkeitsverteilung der Anzahl der Versuche, die erforderlich sind, um in einem Bernoulli-Prozess eine vorgegebene Anzahl von Erfolgen zu erzielen. In der Tabelle werden beide Verteilungen veranschaulicht:
| Deterministisch | Zufällig | Fragestellung | |
|---|---|---|---|
| Binomialverteilung | Versuche | Erfolge | Wie viele Erfolge haben wir in Versuchen? |
| Negative Binomialverteilung | Erfolge | Versuche | Wie viele Versuche sind erforderlich, um Erfolge zu haben? |
Beziehung zur hypergeometrischen Verteilung
Bei der Binomialverteilung werden die ausgewählten Stichproben wieder in die Auswahlmenge zurückgeführt, können also zu einem späteren Zeitpunkt erneut ausgewählt werden. Werden im Gegensatz dazu die Stichproben nicht in die Grundgesamtheit zurückgegeben, kommt die hypergeometrische Verteilung zur Anwendung. Die beiden Verteilungen gehen bei großem Umfang der Grundgesamtheit und geringem Umfang der Stichproben ineinander über. Als Faustregel gilt, dass für auch bei Nichtzurücklegen der Stichproben die Binomialverteilung statt der mathematisch anspruchsvolleren hypergeometrischen Verteilung verwendet werden kann, da beide in diesem Fall nur unwesentlich voneinander abweichende Ergebnisse liefern.
Beziehung zur Multinomialverteilung
Die Binomialverteilung ist ein Spezialfall der Multinomialverteilung.
Beziehung zur Rademacher-Verteilung
Ist Binomialverteilt zum Parameter und , so lässt sich als skalierte Summe von Rademacher-verteilten Zufallsvariablen darstellen:
Dies wird insbesondere bei der symmetrischen einfachen Irrfahrt auf verwendet.
Beziehung zur Panjer-Verteilung
Die Binomialverteilung ist ein Spezialfall der Panjer-Verteilung, welche die Verteilungen Binomialverteilung, Negative Binomialverteilung und Poisson-Verteilung in einer Verteilungsklasse vereint.
Beziehung zur Betaverteilung
Für viele Anwendungen ist es nötig, die Verteilungsfunktion
konkret auszurechnen (beispielsweise bei statistischen Tests oder für Konfidenzintervalle).
Hier hilft die folgende Beziehung zur Betaverteilung:
Diese lautet für ganzzahlige positive Parameter und :
Um die Gleichung
zu beweisen, kann man folgendermaßen vorgehen:
- Die linke und rechte Seite stimmen für überein (beide Seiten sind gleich 1).
- Die Ableitungen nach stimmen für die linke und rechte Seite der Gleichung überein, sie sind nämlich beide gleich .
Beziehung zur Beta-Binomialverteilung
Eine Binomialverteilung, deren Parameter Beta-verteilt ist, nennt man eine Beta-Binomialverteilung. Sie ist eine Mischverteilung.
Beziehung zur Pólya-Verteilung
Die Binomialverteilung ist ein Spezialfall der Pólya-Verteilung (wähle ).
Beispiele
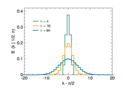
Symmetrische Binomialverteilung (p = 1/2)
- p = 0,5 und n = 4, 16, 64
- Mittelwert abgezogen
- (c) Binomi, CC BY-SA 3.0Skalierung mit Standardabweichung
Dieser Fall tritt auf beim -fachen Münzwurf mit einer fairen Münze (Wahrscheinlichkeit für Kopf gleich der für Zahl, also gleich 1/2). Die erste Abbildung zeigt die Binomialverteilung für und für verschiedene Werte von als Funktion von . Diese Binomialverteilungen sind spiegelsymmetrisch um den Wert :

Dies ist in der zweiten Abbildung veranschaulicht. Die Breite der Verteilung wächst proportional zur Standardabweichung . Der Funktionswert bei , also das Maximum der Kurve, sinkt proportional zu .
Dementsprechend kann man Binomialverteilungen mit unterschiedlichem aufeinander skalieren, indem man die Abszisse durch teilt und die Ordinate mit multipliziert (dritte Abbildung oben).
Die nebenstehende Graphik zeigt noch einmal reskalierte Binomialverteilungen, nun für andere Werte von und in einer Auftragung, die besser verdeutlicht, dass sämtliche Funktionswerte mit steigendem gegen eine gemeinsame Kurve konvergieren. Indem man die Stirling-Formel auf die Binomialkoeffizienten anwendet, erkennt man, dass diese Kurve (im Bild schwarz durchgezogen) eine Gaußsche Glockenkurve ist:
- .
Dies ist die Wahrscheinlichkeitsdichte zur Standardnormalverteilung . Im zentralen Grenzwertsatz wird dieser Befund so verallgemeinert, dass auch Folgen anderer diskreter Wahrscheinlichkeitsverteilungen gegen die Normalverteilung konvergieren.
Die zweite nebenstehende Graphik zeigt die gleichen Daten in einer halblogarithmischen Auftragung. Dies ist dann zu empfehlen, wenn man überprüfen möchte, ob auch seltene Ereignisse, die um mehrere Standardabweichungen vom Erwartungswert abweichen, einer Binomial- oder Normalverteilung folgen.
Ziehen von Kugeln
In einem Behälter befinden sich 80 Kugeln, davon sind 16 gelb. Es wird 5-mal eine Kugel entnommen und anschließend wieder zurückgelegt. Wegen des Zurücklegens ist die Wahrscheinlichkeit, eine gelbe Kugel zu ziehen, bei allen Entnahmen gleich groß, und zwar 16/80 = 1/5. Der Wert gibt die Wahrscheinlichkeit dafür an, dass genau der entnommenen Kugeln gelb sind. Als Beispiel rechnen wir :
In ungefähr 5 % der Fälle zieht man also genau 3 gelbe Kugeln.
| B(k | 0,2; 5) | |
| k | Wahrscheinlichkeit in % |
| 0 | 32,768 |
| 1 | 40,96 |
| 2 | 20,48 |
| 3 | 5,12 |
| 4 | 0,64 |
| 5 | 0,032 |
| ∑ | 100 |
| Erw.Wert | 1 |
| Varianz | 0.8 |
Anzahl der Personen mit Geburtstag am Wochenende
Die Wahrscheinlichkeit, dass eine Person in diesem Jahr an einem Wochenende Geburtstag hat, betrage (der Einfachheit halber) 2/7. In einem Raum halten sich 10 Personen auf. Der Wert gibt (im vereinfachten Modell) die Wahrscheinlichkeit dafür an, dass genau der Anwesenden in diesem Jahr an einem Wochenende Geburtstag haben.
| B(k | 2/7; 10) | |
| k | Wahrscheinlichkeit in % (gerundet) |
| 0 | 3,46 |
| 1 | 13,83 |
| 2 | 24,89 |
| 3 | 26,55 |
| 4 | 18,59 |
| 5 | 8,92 |
| 6 | 2,97 |
| 7 | 0,6797 |
| 8 | 0,1020 |
| 9 | 0,009063 |
| 10 | 0,0003625 |
| ∑ | 100 |
| Erw.Wert | 2,86 |
| Varianz | 2,04 |
Gemeinsamer Geburtstag im Jahr
253 Personen sind zusammengekommen. Der Wert gibt die Wahrscheinlichkeit an, dass genau Anwesende an einem zufällig gewählten Tag Geburtstag haben (ohne Beachtung des Jahrganges).
| B(k | 1/365; 253) | |
| k | Wahrscheinlichkeit in % (gerundet) |
| 0 | 49,95 |
| 1 | 34,72 |
| 2 | 12,02 |
| 3 | 2,76 |
| 4 | 0,47 |
Die Wahrscheinlichkeit, dass „irgendjemand“ dieser 253 Personen, d. h. eine oder mehrere Personen, an diesem Tag Geburtstag hat, beträgt somit .
Bei 252 Personen beträgt die Wahrscheinlichkeit . Das heißt, die Schwelle der Anzahl von Personen, ab der die Wahrscheinlichkeit, dass mindestens eine dieser Personen an einem zufällig gewählten Tag Geburtstag hat, größer als 50 % wird, beträgt 253 Personen (siehe dazu auch Geburtstagsparadoxon).
Die direkte Berechnung der Binomialverteilung kann aufgrund der großen Fakultäten schwierig sein. Eine Näherung über die Poisson-Verteilung ist hier zulässig (). Mit dem Parameter ergeben sich folgende Werte:[13]
| P253/365(k) | |
| k | Wahrscheinlichkeit in % (gerundet) |
| 0 | 50 |
| 1 | 34,66 |
| 2 | 12,01 |
| 3 | 2,78 |
| 4 | 0,48 |
Konfidenzintervall für eine Wahrscheinlichkeit
In einer Meinungsumfrage unter Personen geben Personen an, die Partei A zu wählen. Bestimme ein 95-%-Konfidenzintervall für den unbekannten Anteil der Wähler, die Partei A wählen, in der Gesamtwählerschaft.
Eine Lösung des Problems ohne Rückgriff auf die Normalverteilung findet sich im Artikel Konfidenzintervall für die Erfolgswahrscheinlichkeit der Binomialverteilung.
Auslastungsmodell
Mittels folgender Formel lässt sich die Wahrscheinlichkeit dafür errechnen, dass von Personen eine Tätigkeit, die durchschnittlich Minuten pro Stunde dauert, gleichzeitig ausführen.
Zufallszahlen
Zufallszahlen zur Binomialverteilung werden üblicherweise mit Hilfe der Inversionsmethode erzeugt.
Alternativ kann man auch ausnutzen, dass die Summe von Bernoulli-verteilten Zufallsvariablen binomialverteilt ist. Dazu erzeugt man Bernoulli-verteilte Zufallszahlen und summiert sie auf; das Ergebnis ist eine binomialverteilte Zufallszahl.
Bezeichnungen
Der Aufruf der Wahrscheinlichkeitsfunktion der Binomialverteilung bei Taschenrechnern und Mathematischer Software geschieht meistens mit binom, pdfbin oder Binomialpdf (Binomial probability density function). Die kumulierte Verteilungsfunktion wird mit cdfbin oder Binomialcdf (Binomial cumulative distribution function) abgekürzt.[14]
Weblinks
- Bernoulli-Versuche und Binomialverteilung
- Rechner für einfache und kumulierte Wahrscheinlichkeiten der Binomialverteilung
- Berechnung der Binomialverteilung für einfache und kumulierte Wahrscheinlichkeiten (englisch)
- Umfangreiches Tabellenwerk (PDF; 10 MB)
- Binomial- und Normalverteilung – Online-Lehrgang mit dynamischen Arbeitsblättern (Java-Plugin benötigt)
- Interaktive Simulation Münzwurf – inkl. Aufgabenstellungen (HTML5 ohne Plugin)
- Interaktive Animation – Universität Konstanz (Java-Plugin benötigt)
- Interaktive Animation (Flash-Plugin benötigt)
- Earliest Known Uses of Some of the Words of Probability & Statistics – Kees Verduin.
- Lernvideo für die Oberstufe
- Statistische Fehler (Ausführliche Erläuterung aus der Universität Ulm)
Einzelnachweise
- ↑ Binomialverteilung. In: P. H. Müller (Hrsg.): Lexikon der Stochastik – Wahrscheinlichkeitsrechnung und mathematische Statistik. 5. Auflage. Akademie-Verlag, Berlin 1991, ISBN 978-3-05-500608-1, S. 39.
- ↑ Peter Kissel: MAC08 Stochastik (Teil 2). Studiengemeinschaft Darmstadt 2014, S. 12.
- ↑ Bigalke, Köhler: Mathematik 13.2 Grund- und Leistungskurs. Cornelsen, Berlin 2000, S. 130.
- ↑ George Udny Yule: An Introduction to the Theory of Statistics. Griffin, London 1911, S. 287.
- ↑ Peter Kissel: MAC08 Stochastik. Teil 2. Studiengemeinschaft Darmstadt 2014, S. 23.
- ↑ Bigalke,/ Köhler: Mathematik 13.2 Grund- und Leistungskurs. Cornelsen, Berlin 2000, S. 144 ff.
- ↑ P. Neumann: Über den Median der Binomial- and Poissonverteilung. In: Wissenschaftliche Zeitschrift der Technischen Universität Dresden. 19. Jahrgang, 1966, S. 29–33.
- ↑ Lord, Nick. (July 2010). Binomial averages when the mean is an integer, The Mathematical Gazette 94, 331–332.
- ↑ a b R. Kaas, J.M. Buhrman: Mean, Median and Mode in Binomial Distributions. In: Statistica Neerlandica. 34. Jahrgang, Nr. 1, 1980, S. 13–18, doi:10.1111/j.1467-9574.1980.tb00681.x (englisch).
- ↑ a b K. Hamza: The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions. In: Statistics & Probability Letters. 23. Jahrgang, 1995, S. 21–25, doi:10.1016/0167-7152(94)00090-U (englisch).
- ↑ Peter Harremoës: Binomial and Poisson Distributions as Maximum Entropy Distributions. In: IEEE Transactions on Information Theory. 47. Jahrgang. IEEE Information Theory Society, 2001, S. 2039–2041, doi:10.1109/18.930936 (englisch).
- ↑ M. Brokate, N. Henze, F. Hettlich, A. Meister, G. Schranz-Kirlinger, Th. Sonar: Grundwissen Mathematikstudium: Höhere Analysis, Numerik und Stochastik. Springer-Verlag, 2015, S. 890.
- ↑ Im konkreten Fall muss man für die Binomialverteilung ausrechnen und für die Poisson-Verteilung . Beides ist mit dem Taschenrechner einfach. Bei einer Rechnung mit Papier und Bleistift benötigt man mit der Exponentialreihe 8 oder 9 Glieder für den Wert der Poisson-Verteilung, während man für die Binomialverteilung durch mehrfaches Quadrieren auf die 256. Potenz kommt und dann noch durch die dritte Potenz teilt.
- ↑ Scilab Online Help – Statistics. Abgerufen am 13. Januar 2022.
Auf dieser Seite verwendete Medien
Autor/Urheber: Schlurcher
Binomial Verteilung zu den Parametern 0.1 (blau), 0.5 (grün) und 0.8 (rot).
Binomial distribution cumulative distribution function
The area of all bars in a row is always 1.
Autor/Urheber: Der ursprünglich hochladende Benutzer war Binomi in der Wikipedia auf Deutsch, Lizenz: GFDL
selbstgebraut
Autor/Urheber: Weialawaga in der Wikipedia auf Deutsch, Lizenz: GFDL
selbstgemacht, GNU-FDL
Autor/Urheber: Der ursprünglich hochladende Benutzer war Binomi in der Wikipedia auf Deutsch, Lizenz: CC BY-SA 3.0
selbst geplottet
Binomial distribution probability mass function