Basler Problem

Das Basler Problem ist ein mathematisches Problem, das für längere Zeit ungelöst war und mit dem sich anfangs vor allem Basler Mathematiker befassten. Es handelt sich um die Frage nach der Summe der reziproken Quadratzahlen, also nach dem Wert der Reihe

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots =1+{\frac {1}{4}}+{\frac {1}{9}}+{\frac {1}{16}}+\cdots .}$

Es wurde 1735 durch Leonhard Euler gelöst, der den Reihenwert ${\displaystyle {\tfrac {\pi ^{2}}{6}}\approx 1{,}644934}$ fand. Man kann dies auch als Suche nach dem Wert ${\displaystyle \zeta (2)}$ der Riemannschen ζ-Funktion an der Stelle 2 auffassen, die definitionsgemäß durch die angegebene unendliche Reihe dargestellt wird.

Das Basler Problem ist äquivalent zu

${\displaystyle \sum _{k=0}^{\infty }{\frac {1}{{(2k+1)}^{2}}}={\frac {{\pi }^{2}}{8}}}$

wegen

${\displaystyle {\frac {3}{4}}\zeta (2)=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}-\sum _{m=1}^{\infty }{\frac {1}{{(2m)}^{2}}}=\sum _{k=0}^{\infty }{\frac {1}{{(2k+1)}^{2}}}.}$

Lösungsversuche

1644 fragte sich der Italiener Pietro Mengoli, ob diese Summe konvergiere, und wenn ja, gegen welchen Wert, konnte diese Frage aber nicht beantworten. Etwas später erfuhr der Basler Mathematiker Jakob I Bernoulli von diesem Problem, fand jedoch auch keine Lösung (1689). Daraufhin versuchten sich mehrere Mathematiker an der Fragestellung, waren aber alle erfolglos. 1726 begann Leonhard Euler, ebenfalls Basler Mathematiker und Schüler von Jakob Bernoullis Bruder Johann, sich mit dem Problem zu befassen. 1735 fand er die Lösung und veröffentlichte sie in seinem Werk De Summis Serierum Reciprocarum.^[1] Die überraschende Lösung, die ${\displaystyle \pi }$ enthielt (bis dahin hatten andere Mathematiker durch numerische Versuche nur gefunden, dass die Lösung nahe ${\displaystyle {\frac {8}{5}}}$ liegen musste), trug wesentlich dazu bei, Eulers Name als Mathematiker bekannt zu machen.^[2] Der Beweis erschien zwar erst 1740 im Druck, verbreitete sich aber schon bald nach seiner Entdeckung unter den führenden Mathematikern im damaligen Europa.^[3] Euler hatte sich dem Problem seit 1728 gewidmet. Vor dem exakten Beweis war es ihm durch numerische Rechnungen gelungen, den Wert der Reihe bis auf 20 Dezimalplätze genau zu berechnen (1732), was in ihm schon eine Vermutung über den genauen Wert entstehen ließ.^[4] Ein zweiter Beweis von Euler ist von 1741.^[5]

Es gibt viele verschiedene Beweise für die Lösung des Basler Problems. In Das Buch der Beweise^[6] werden neben einem (unten dargestellten) Beweis von William LeVeque (1956)^[7] Beweise von Jonathan Borwein und Peter Borwein dargestellt (aus einer Übungsaufgabe in ihrem Buch Pi and the AGM von 1987, er basiert auf einer „Quadrierung“ der Leibniz-Reihe),^[8] ein elementarer Beweis von Akiwa Moissejewitsch Jaglom und Isaak Moissejewitsch Jaglom (1954, Ausgangspunkt ist eine Identität für eine Summe von Quadraten der Kotangensfunktion und wird unten dargestellt)^[9], der mehrfach wiederentdeckt wurde und sich schon bei Augustin-Louis Cauchy 1821 findet (Cours d'Analyse, Note VIII), und ein Beweis von Frits Beukers, A. C. Kolk und Eugenio Calabi (1993), bei dem ein Doppelintegral durch geschickte Koordinatentransformation ausgewertet wird.^[10][11] Ein Beweis aus der komplexen Analysis nutzt das Residuenkalkül für die Auswertung eines Integrals über die Funktion ${\displaystyle f(z)=\pi {\frac {\cot(\pi z)}{z^{2}}}}$, die Pole genau an den ganzen Zahlen hat.^[12]

Euler behandelte 1755 auch allgemein Werte der Zetafunktion bei geradzahligen Werten mit Hilfe der Partialbruchentwicklung der Kotangensfunktion.^[13][14]

Lösungswege

Eulers erste Lösung

Für seine ursprüngliche Lösung^[15] betrachtete Euler die Taylorreihe der Kardinalsinusfunktion, also

${\displaystyle \operatorname {si} (x)={\frac {\sin(x)}{x}}=1-{\frac {x^{2}}{3!}}+{\frac {x^{4}}{5!}}-{\frac {x^{6}}{7!}}+-\cdots }$

und setzte sie mit der Produktdarstellung jener Funktion gleich:

${\displaystyle {\frac {\sin(x)}{x}}=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)=\left(1-{\frac {x^{2}}{\pi ^{2}}}\right)\left(1-{\frac {x^{2}}{4\pi ^{2}}}\right)\left(1-{\frac {x^{2}}{9\pi ^{2}}}\right)\cdots =1-{\frac {x^{2}}{3!}}+{\frac {x^{4}}{5!}}-{\frac {x^{6}}{7!}}+-\cdots }$

Beim (hypothetischen) Ausmultiplizieren des unendlichen Produkts betrachtete er nur diejenigen Produkte, welche ${\displaystyle 1}$ und ${\displaystyle x^{2}}$ enthalten. Da es keine weitere Möglichkeit gibt, dass ein Term ein quadratisches Glied enthalten kann, müssen die beiden quadratischen Terme auf den jeweiligen Seiten gleich sein, also

${\displaystyle -x^{2}\left({\frac {1}{\pi ^{2}}}+{\frac {1}{2^{2}\pi ^{2}}}+{\frac {1}{3^{2}\pi ^{2}}}+{\frac {1}{4^{2}\pi ^{2}}}+\cdots \right)=-{\frac {x^{2}}{3!}}=-{\frac {x^{2}}{6}}}$.

Daraus folgerte Euler seine Lösung:

${\displaystyle 1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}.}$

Für eine strenge Begründung der Produktdarstellung ist allerdings der erst später bewiesene Weierstraßsche Produktsatz nötig.

Geometrische Lösung

Diese Lösung benutzt den Satz von Thales, den Kreiswinkelsatz, den inversen Satz des Pythagoras und das Abstandsquadratgesetz.^[16][17][18]

Abb. 1: Illustration zum Satz von Thales (blau), Kreiswinkelsatz (grün) und inversen Satz des Pythagoras (gelb und rot)	Abb. 2: Die Lichtmenge, die das Segelboot in Summe von den schwarzen Leuchttürmen empfängt, ist dieselbe, die es vom roten Leuchtturm erhält

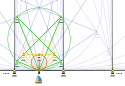
Der rote Kreisbogen in Abbildung 2 über dem Durchmesser vom Segelboot zum roten Leuchtturm hat die Länge 1, und der Umfang des roten Kreises ist 2, womit sein Durchmesser 2/π ist. Das Segelboot empfängt vom roten Leuchtturm eine Lichtmenge C, die nach dem Abstandsquadratgesetz umgekehrt proportional zum Abstandsquadrat ist oder, der Einfachheit halber, gleich dem Kehrwert des Abstandsquadrates ist, womit hier C=π²/4 ist.

Im Folgenden leuchten alle betrachteten Leuchttürme so hell wie der rote, bezeichnet Intensität die vom Segelboot empfangene Lichtmenge und Bogenabstand die Länge des zwischen zwei Orten liegenden Kreisbogens. Der rote Leuchtturm hat in Abbildung 2 den Bogenabstand 1 zum Segelboot und die Intensität C. Die beiden gelben Leuchttürme liegen auf dem doppelt so großen gelben Kreis, sodass sie den Bogenabstand 2 zueinander und den Bogenabstand 1 zum Segelboot haben.

Die Intensität der beiden gelben Leuchttürme ist in Summe dieselbe wie die des roten Leuchtturms. Denn die gelben Leuchttürme erzeugen mit dem Segelboot nach dem Satz von Thales ein rechtwinkliges Dreieck und der rote Leuchtturm liegt am Fußpunkt der Höhe des Segelbootes über der Hypotenuse des Dreiecks, womit die Aussage aus dem inversen Satz des Pythagoras und dem Abstandsquadratgesetz folgt, siehe Abbildung 1.

Ebenso ist die Intensität der vier grünen Leuchttürme in Abbildung 2 in Summe dieselbe wie die der beiden gelben Leuchttürme, deren Intensität in Summe der des einen roten Leuchtturms entspricht. Die grünen Leuchttürme liegen nach dem Kreiswinkelsatz ebenfalls im Bogenabstand 2 zueinander und der nächstgelegene im Bogenabstand 1 zum Segelboot, siehe Abbildung 1. Dieses Verfahren kann durch Verdoppelung der Anzahl der Leuchttürme auf doppelt so großen Kreisen immer weiter fortgesetzt werden, wobei

• der Bogenabstand des Segelbootes zum nächstgelegenen Leuchtturm immer 1 ist,
• der Bogenabstand zwischen zwei benachbarten Leuchttürmen immer 2 ist,
• die Intensität aller Leuchttürme auf dem Kreis in Summe immer gleich derjenigen des roten Leuchtturms ist und
• die Leuchttürme, die einen bestimmten Bogenabstand vom Segelboot haben, Endpunkte von Durchmessern sind, die sich einer Senkrechten im Bild immer mehr nähern und an deren anderem Endpunkt ein Leuchtturm scheint, der immer weniger zur Intensität beiträgt.

Indem der Trägerkreis der Leuchttürme immer größer wird, nähert er sich immer mehr einer Geraden an, schwarz in Abbildung 2, auf der Leuchttürme (ebenfalls schwarz) immer im Abstand 2 an den Stellen ±1, ±3, ±5,… stehen, wenn das Segelboot im Ursprung schwimmt, und nur diese Leuchttürme tragen nennenswert zur Intensität bei. Daher ist die Intensität der schwarzen Leuchttürme in Summe gleich der des roten Leuchtturms C=π²/4.

Wenn die schwarzen Leuchttürme links vom Segelboot ausgeschaltet werden, halbiert sich die Intensität zu ${\displaystyle \textstyle {\frac {\pi ^{2}}{8}}}$ und entspricht der Summe

${\displaystyle h={\frac {1}{1^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{5^{2}}}+\dots ={\frac {\pi ^{2}}{8}}.}$

Beim Basler Problem ist

${\displaystyle H={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\dots }$

gesucht, was Leuchttürmen an den Stellen 1, 2, 3,… im Abstand 1 entspricht. Werden deren Abstände verdoppelt, viertelt sich nach dem Abstandsquadratgesetz die Intensität:

${\displaystyle {\frac {H}{4}}={\frac {1}{2^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{6^{2}}}+\dots }$

Addition von h ergibt das gesuchte:

${\displaystyle {\begin{aligned}{\frac {H}{4}}+h=&\ {\frac {1}{2^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{6^{2}}}+\dots +{\frac {1}{1^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{5^{2}}}+\dots \\=&\ {\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+{\frac {1}{5^{2}}}+{\frac {1}{6^{2}}}+\dots =H\\\iff H-{\frac {H}{4}}=&\ {\frac {3}{4}}H=h={\frac {\pi ^{2}}{8}},\end{aligned}}}$

was äquivalent zu ${\displaystyle \textstyle H={\frac {\pi ^{2}}{6}}}$ ist.

Lösung über den Satz von Fubini

Die unendliche Summe der Quadratzahlkehrwerte steht in enger Beziehung zu der unendlichen Summe der sich an ungerader Stelle befindenden Summanden. Es gilt

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {4}{3}}\sum _{k=0}^{\infty }{\frac {1}{(2k+1)^{2}}}.}$

Die Summe der geraden Stellen ist das Viertel von der gesamten Summe. Analog ist die Summe der ungeraden Stellen drei Viertel von der gesamten Summe. Folglich ist die gesamte Summe vier Drittel von der Summe der ungeraden Stellen. Im nun Folgenden wird die Summe in ein Integral verwandelt:

${\displaystyle \sum _{k=0}^{\infty }{\frac {1}{(2k+1)^{2}}}=\sum _{k=0}^{\infty }\int _{0}^{1}{\frac {x^{2k}}{(2k+1)}}\mathrm {d} x=\int _{0}^{1}\sum _{k=0}^{\infty }{\frac {x^{2k}}{(2k+1)}}\mathrm {d} x=\int _{0}^{1}{\frac {\operatorname {artanh} (x)}{x}}\mathrm {d} x.}$

Also gilt folgender Ausdruck:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {4}{3}}\int _{0}^{1}{\frac {\operatorname {artanh} (x)}{x}}\mathrm {d} x.}$

Das gezeigte Integral besitzt keine elementare Stammfunktion. Aber mit dem Satz von Fubini lässt sich dieses Integral^[19] lösen. Erster möglicher Lösungsweg:

${\displaystyle \int _{0}^{1}{\frac {\operatorname {artanh} (x)}{x}}\mathrm {d} x=\int _{0}^{\infty }{\frac {\operatorname {arsinh} (x)}{2x{\sqrt {x^{2}+1}}}}\mathrm {d} x=\int _{0}^{\infty }\int _{0}^{1}{\frac {1}{2(-x^{2}y^{2}+x^{2}+1)}}\mathrm {d} y\mathrm {d} x=\int _{0}^{1}\int _{0}^{\infty }{\frac {1}{2(-x^{2}y^{2}+x^{2}+1)}}\mathrm {d} x\mathrm {d} y=\int _{0}^{1}{\frac {\pi }{4{\sqrt {1-y^{2}}}}}\mathrm {d} y={\frac {\pi ^{2}}{8}}.}$

Im ersten Schritt wurde wie folgt substituiert:

${\displaystyle x\mapsto {\frac {x}{{\sqrt {x^{2}+1}}+1}}.}$

Denn folgender Zusammenhang gilt:

${\displaystyle [{\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {x}{{\sqrt {x^{2}+1}}+1}}]{\frac {\operatorname {artanh} (w)}{w}}(w={\frac {x}{{\sqrt {x^{2}+1}}+1}})={\frac {\operatorname {arsinh} (x)}{2x{\sqrt {x^{2}+1}}}}.}$

Zweiter möglicher Lösungsweg:

Diese Ableitung ist gültig:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} y}}\,{\frac {1}{x}}{\biggl [}\operatorname {artanh} (x)-\operatorname {artanh} {\biggl (}{\frac {x\,{\sqrt {1-y^{2}}}}{\sqrt {1-x^{2}y^{2}}}}{\biggr )}{\biggr ]}={\frac {y}{\sqrt {(1-x^{2}y^{2})(1-y^{2})}}}}$

Somit kann dann diese Integralkette über den Satz von Fubini aufgestellt werden:

${\displaystyle \int _{0}^{1}{\frac {\operatorname {artanh} (x)}{x}}\,\mathrm {d} x=\int _{0}^{1}\int _{0}^{1}{\frac {y}{\sqrt {(1-x^{2}y^{2})(1-y^{2})}}}\,\mathrm {d} y\,\mathrm {d} x=\int _{0}^{1}\int _{0}^{1}{\frac {y}{\sqrt {(1-x^{2}y^{2})(1-y^{2})}}}\,\mathrm {d} x\,\mathrm {d} y=\int _{0}^{1}{\frac {\operatorname {arcsin} (y)}{\sqrt {1-y^{2}}}}\,\mathrm {d} y={\frac {\pi ^{2}}{8}}.}$

Als Stammfunktion im letzten Schritt diente die Hälfte vom Quadrat des Arcussinus. Insgesamt gilt somit der auf dieser Seite behandelte Zusammenhang:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {\pi ^{2}}{6}}.}$

Der Beweis über den Satz von Fubini ist von James D. Harper veröffentlicht worden.^[20]

Über ein Doppelintegral

Der Beweis über ein Doppelintegral erscheint als eine Übung in William J. LeVeques Lehrbuch zur Zahlentheorie von 1956. Darin schreibt er zu dem Problem: „Ich habe nicht die geringste Ahnung, woher dieses Problem stammt, aber ich bin mir ziemlich sicher, dass es bei mir nicht seinen Ursprung hatte.“

Über die geometrische Reihe erhält man zuerst die Darstellung

${\displaystyle \zeta (2)=\int _{0}^{1}\int _{0}^{1}{\frac {\mathrm {d} x\mathrm {d} y}{1-xy}}.}$

Mittels einer Variablensubstitution ${\displaystyle u={\frac {y+x}{2}}}$ und ${\displaystyle v={\frac {y-x}{2}}}$ gelangt man zu

${\displaystyle \zeta (2)=4\int _{0}^{\frac {1}{2}}\left(\int _{0}^{u}{\frac {\mathrm {d} v}{1-u^{2}+v^{2}}}\right)\mathrm {d} u+4\int _{\frac {1}{2}}^{1}\left(\int _{0}^{1-u}{\frac {\mathrm {d} v}{1-u^{2}+v^{2}}}\right)\mathrm {d} u,}$

wobei sich die inneren Integrale mit Hilfe des Arkustangens auflösen lassen zu

${\displaystyle \zeta (2)=4\int _{0}^{\frac {1}{2}}{\frac {1}{\sqrt {1-u^{2}}}}\arctan \left({\frac {u}{\sqrt {1-u^{2}}}}\right)\mathrm {d} u+4\int _{\frac {1}{2}}^{1}{\frac {1}{\sqrt {1-u^{2}}}}\arctan \left({\frac {1-u}{\sqrt {1-u^{2}}}}\right)\mathrm {d} u.}$

Mit ${\displaystyle g(u)=\arctan \left({\frac {u}{\sqrt {1-u^{2}}}}\right)}$ und ${\displaystyle h(u)=\arctan \left({\frac {1-u}{\sqrt {1-u^{2}}}}\right)}$ erhält man die Schreibweise

${\displaystyle \zeta (2)=4\int _{0}^{\frac {1}{2}}g'(u)g(u)\mathrm {d} u+4\int _{\frac {1}{2}}^{1}h'(u)h(u)\mathrm {d} u=2{\Big [}g(u)^{2}{\Big ]}_{0}^{\frac {1}{2}}+2{\Big [}h(u)^{2}{\Big ]}_{\frac {1}{2}}^{1}={\frac {\pi ^{2}}{6}}.}$

Über die alternierende Differenz

Der Wert der Reihe ist das Doppelte der alternierenden Differenz der Kehrwerte, die gleich dem bestimmten Integral von ln(1+x)/x im Intervall von null bis eins ist. Dieses Integral kann mit dem Satz von Fubini berechnet werden und führt auf die Lösung. Dies soll im Folgenden mathematisch dargestellt werden.

Die gesuchte Summe wird in Summanden mit ungeradem und geradem Laufindex aufgeteilt

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=\sum _{n=1}^{\infty }{\frac {1}{(2\,n-1)^{2}}}+\sum _{n=1}^{\infty }{\frac {1}{(2\,n)^{2}}}=\sum _{n=1}^{\infty }{\frac {1}{(2\,n-1)^{2}}}+{\frac {1}{4}}\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}}$

und das Resultat kombiniert zu

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=2\left[\sum _{n=1}^{\infty }{\frac {1}{(2\,n-1)^{2}}}+{\frac {1}{4}}\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}\right]-{\frac {4}{4}}\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=2\sum _{m=1}^{\infty }{\biggl [}{\frac {1}{(2m-1)^{2}}}-{\frac {1}{(2m)^{2}}}{\biggr ]}}$

oder straffer

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=2\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {1}{k^{2}}}}$

Mit dem für ${\displaystyle k\geq 1}$ gültigen bestimmten Integral

${\displaystyle \int _{0}^{1}{\frac {x^{k-1}}{k}}\mathrm {d} x=\left[{\frac {x^{k}}{k^{2}}}\right]_{0}^{1}={\frac {1}{k^{2}}}}$

entsteht die Integralidentität

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=2\sum _{k=1}^{\infty }(-1)^{k+1}\int _{0}^{1}{\frac {x^{k-1}}{k}}\mathrm {d} x=2\int _{0}^{1}{\frac {1}{x}}\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {x^{k}}{k}}\mathrm {d} x,}$

die sich mit der Potenzreihe des Logarithmus-Naturalis wie folgt ausdrücken lässt:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=2\int _{0}^{1}{\frac {1}{x}}\ln(1+x)\,\mathrm {d} x}$

Dieses Logarithmus-Naturalis-Integral kann erneut mit dem Satz von Fubini bestimmt werden:

${\displaystyle {\begin{aligned}&\int _{0}^{1}{\frac {1}{x}}\ln(x+1)\,\mathrm {d} x\\&=\int _{0}^{1}\int _{0}^{1}\left[{\frac {4}{3(x^{2}+2xy+1)}}+{\frac {2x}{3(x^{2}y+1)}}-{\frac {1}{3(xy+1)}}\right]\mathrm {d} y\,\mathrm {d} x\\&=\int _{0}^{1}\int _{0}^{1}\left[{\frac {4}{3(x^{2}+2xy+1)}}+{\frac {2x}{3(x^{2}y+1)}}-{\frac {1}{3(xy+1)}}\right]\mathrm {d} x\,\mathrm {d} y\\&=\int _{0}^{1}{\frac {4}{3{\sqrt {1-y^{2}}}}}{\biggl [}\arctan {\biggl (}{\frac {1+y}{\sqrt {1-y^{2}}}}{\biggr )}-\arctan {\biggl (}{\frac {y}{\sqrt {1-y^{2}}}}{\biggr )}{\biggr ]}\,\mathrm {d} y\\&=\int _{0}^{1}{\frac {2\arccos(y)}{3{\sqrt {1-y^{2}}}}}\,\mathrm {d} y=-{\frac {1}{3}}{\bigg [}\arccos(y)^{2}{\bigg ]}_{0}^{1}={\frac {\pi ^{2}}{12}}\end{aligned}}}$

Denn es ist:

${\displaystyle {\begin{aligned}&\int \left({\frac {4}{3(x^{2}+2xy+1)}}+{\frac {2x}{3(x^{2}y+1)}}-{\frac {1}{3(xy+1)}}\right)\mathrm {d} y=\dots \\&\qquad \dots ={\frac {2}{3x}}\ln(x^{2}+2xy+1)+{\frac {2}{3x}}\ln(x^{2}y+1)-{\frac {1}{3x}}\ln(xy+1)=:F(y)\\&{\bigg [}F(y){\bigg ]}_{0}^{1}={\frac {2}{3x}}\ln \left((x+1)^{2}\right)+{\frac {2}{3x}}\ln(x^{2}+1)-{\frac {1}{3x}}\ln(x+1)-{\frac {2}{3x}}\ln(x^{2}+1)={\frac {1}{x}}\ln(x+1)\\&\int \left({\frac {4}{3(x^{2}+2xy+1)}}+{\frac {2x}{3(x^{2}y+1)}}-{\frac {1}{3(xy+1)}}\right)\mathrm {d} x=\dots \\&\qquad \dots ={\frac {4}{3{\sqrt {1-y^{2}}}}}\arctan {\biggl (}{\frac {x+y}{\sqrt {1-y^{2}}}}{\biggr )}-{\frac {1}{3y}}\ln {\biggl (}{\frac {xy+1}{x^{2}y+1}}{\biggr )}\\&\int {\frac {2\arccos(y)}{3{\sqrt {1-y^{2}}}}}\mathrm {d} y=-{\frac {1}{3}}\arccos(y)^{2}\end{aligned}}}$

Und mit den Formeln für gegenseitige Darstellung, die Additionstheoreme und Doppelwinkelfunktionen aus der Trigonometrie sowie den Abkürzungen ${\displaystyle a={\frac {1+y}{\sqrt {1-y^{2}}}}=\tan \alpha ,b={\frac {y}{\sqrt {1-y^{2}}}}=\tan \beta }$ als auch ${\displaystyle \gamma =\alpha -\beta =\arctan {\Big (}{\tfrac {1+y}{\sqrt {1-y^{2}}}}{\Big )}-\arctan {\Big (}{\tfrac {y}{\sqrt {1-y^{2}}}}{\Big )}}$ zeigt sich noch:

${\displaystyle {\begin{aligned}y=&{\frac {2}{1+{\sqrt {\frac {1-y}{1+y}}}^{2}}}-1={\frac {2}{1+\left({\frac {a-b}{1+ab}}\right)^{2}}}-1={\frac {2}{1+\left({\frac {\tan(\alpha )-\tan(\beta )}{1+\tan(\alpha )\tan(\beta )}}\right)^{2}}}-1\\=&{\frac {2}{1+\tan(\alpha -\beta )^{2}}}-1={\frac {2}{1+\tan(\gamma )^{2}}}-1=2\cos(\gamma )^{2}-1=\cos(2\gamma )\end{aligned}}}$

Es gilt somit:

${\displaystyle \int _{0}^{1}{\frac {1}{x}}\ln(x+1)\,\mathrm {d} x={\frac {\pi ^{2}}{12}}}$

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=2\int _{0}^{1}{\frac {1}{x}}\ln(x+1)\,\mathrm {d} x}$

Und dann gilt:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {\pi ^{2}}{6}}}$

Über die Reihenentwicklung des Arkussinus

Der Beweis über die Reihenentwicklung des Arkussinus entspricht dem zweiten Beweis von Euler von 1741.

Es gilt folgende Formel:

${\displaystyle (2k+2)\int _{0}^{1}{\frac {x^{2k+1}}{\sqrt {1-x^{2}}}}\,\mathrm {d} x-(2k+3)\int _{0}^{1}{\frac {x^{2k+3}}{\sqrt {1-x^{2}}}}\,\mathrm {d} x}$

${\displaystyle =\int _{0}^{1}{\biggl [}(2k+2){\frac {x^{2k+1}}{\sqrt {1-x^{2}}}}-(2k+3){\frac {x^{2k+3}}{\sqrt {1-x^{2}}}}{\biggr ]}\,\mathrm {d} x}$

${\displaystyle =\int _{0}^{1}{\frac {\mathrm {d} }{\mathrm {d} x}}\left(x^{2k+2}{\sqrt {1-x^{2}}}\right)\,\mathrm {d} x=\left[x^{2k+2}{\sqrt {1-x^{2}}}\right]_{0}^{1}=0.}$

Daraus folgt für alle ${\displaystyle k\in \mathbb {N} _{0}}$:

${\displaystyle \int _{0}^{1}{\frac {x^{2k+3}}{\sqrt {1-x^{2}}}}\mathrm {d} x={\frac {2k+2}{2k+3}}\int _{0}^{1}{\frac {x^{2k+1}}{\sqrt {1-x^{2}}}}\mathrm {d} x.}$

Zusammen mit dem initialen Wert ${\displaystyle \textstyle \int _{0}^{1}{\frac {x}{\sqrt {1-x^{2}}}}\mathrm {d} x=1}$ kann durch Induktion für alle ${\displaystyle k\in \mathbb {N} _{0}}$

${\displaystyle \int _{0}^{1}{\frac {x^{2k+1}}{\sqrt {1-x^{2}}}}\mathrm {d} x={\frac {4^{k}(k!)^{2}}{(2k)!(2k+1)}}}$

gezeigt werden. Außerdem gilt mittels Taylor-Entwicklung:

${\displaystyle \sum _{k=0}^{\infty }{\frac {(2k)!}{4^{k}(k!)^{2}(2k+1)}}x^{2k+1}=\arcsin(x).}$

Durch Synthese der beiden zuletzt genannten Formeln folgt:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {4}{3}}\sum _{k=0}^{\infty }{\frac {1}{(2k+1)^{2}}}}$

${\displaystyle ={\frac {4}{3}}\sum _{k=0}^{\infty }{\frac {(2k)!}{4^{k}(k!)^{2}(2k+1)}}\,{\frac {4^{k}(k!)^{2}}{(2k)!(2k+1)}}}$

${\displaystyle ={\frac {4}{3}}\sum _{k=0}^{\infty }{\frac {(2k)!}{4^{k}(k!)^{2}(2k+1)}}\int _{0}^{1}{\frac {x^{2k+1}}{\sqrt {1-x^{2}}}}\mathrm {d} x}$

${\displaystyle ={\frac {4}{3}}\int _{0}^{1}\sum _{k=0}^{\infty }{\frac {(2k)!}{4^{k}(k!)^{2}(2k+1)}}\,{\frac {x^{2k+1}}{\sqrt {1-x^{2}}}}\mathrm {d} x}$

${\displaystyle ={\frac {4}{3}}\int _{0}^{1}{\frac {\arcsin(x)}{\sqrt {1-x^{2}}}}\mathrm {d} x}$

${\displaystyle ={\frac {4}{3}}{\biggl [}{\frac {1}{2}}\arcsin(x)^{2}{\biggr ]}_{x=0}^{x=1}}$

${\displaystyle ={\frac {\pi ^{2}}{6}}.}$

Über eine Kotangenssumme

Dieser Beweis findet sich schon bei Cauchy und wurde mehrfach neu entdeckt (darunter durch die Gebrüder Jaglom). Ausgangspunkt ist die Kotangenssumme:

${\displaystyle \sum _{n=1}^{m}\cot \left({\frac {\pi n}{2m+1}}\right)^{2}={\frac {m(2m-1)}{3}}.}$

Dies kann auf folgende Weise erklärt werden:

${\displaystyle \tan[(2m+1)\varphi ]=\left[\sum _{k=0}^{m}{\binom {2m+1}{2k+1}}(-1)^{k}\cot(\varphi )^{2m-2k}\right]\left[\sum _{k=0}^{m}{\binom {2m+1}{2k}}(-1)^{k}\cot(\varphi )^{2m+1-2k}\right]^{-1}.}$

Diese Gleichung resultiert aus dem Additionstheorem der Tangens-Funktion.

Deswegen hat die Gleichungen

${\displaystyle \sum _{k=0}^{m}{\binom {2m+1}{2k+1}}(-1)^{k}x^{m-k}=0}$

folgende Lösungen:

${\displaystyle x_{n}=\cot \left({\frac {\pi n}{2m+1}}\right)^{2},\qquad n=1,2,\cdots ,m.}$

Da die obere Gleichung vom Grad ${\displaystyle m}$ ist und die Werte ${\displaystyle x_{n}}$ paarweise verschieden sind, bilden sie die vollständige Lösungsmenge. Der Satz von Vieta besagt, dass man die negative Summe aller Lösungen der gesamten Lösungsmenge dadurch erhält, dass man den Koeffizient des rangmäßig zweithöchsten Gliedes durch den Koeffizient des rangmäßig höchsten Gliedes teilt. Das rangmäßig höchste Glied nimmt den Wert 1 aus ${\displaystyle 2m+1}$ an. Das rangmäßig zweithöchste Glied nimmt das Negative des Wertes 3 aus ${\displaystyle 2m+1}$ an. Somit gilt folgende Formel:

${\displaystyle \sum _{n=1}^{m}\cot \left({\frac {\pi n}{2m+1}}\right)^{2}={\binom {2m+1}{3}}{\binom {2m+1}{1}}^{-1}={\frac {m(2m-1)}{3}}.}$

Diese kann auch elementar unter Verwendung der Eulerschen Identität gezeigt werden.

Deswegen gilt Folgendes:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=\sum _{n=1}^{\infty }\lim _{m\rightarrow \infty }{\frac {\pi ^{2}}{(2m+1)^{2}}}\cot \left({\frac {\pi n}{2m+1}}\right)^{2}}$

${\displaystyle =\lim _{m\rightarrow \infty }\sum _{n=1}^{m}{\frac {\pi ^{2}}{(2m+1)^{2}}}\cot \left({\frac {\pi n}{2m+1}}\right)^{2}}$

${\displaystyle =\lim _{m\rightarrow \infty }{\frac {\pi ^{2}}{(2m+1)^{2}}}\sum _{n=1}^{m}\cot \left({\frac {\pi n}{2m+1}}\right)^{2}}$

${\displaystyle =\lim _{m\rightarrow \infty }{\frac {\pi ^{2}}{(2m+1)^{2}}}\,{\frac {m(2m-1)}{3}}={\frac {\pi ^{2}}{6}}.}$

Beweis über Fourier-Reihen

Der Satz von Parseval angewandt auf die Funktion ${\displaystyle f(x)=x}$ ergibt:

${\displaystyle \sum _{n=-\infty }^{\infty }|c_{n}|^{2}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }x^{2}\,\mathrm {d} x}$

mit

${\displaystyle c_{n}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }xe^{-inx}\,\mathrm {d} x={\frac {n\pi \cos(n\pi )-\sin(n\pi )}{\pi n^{2}}}i={\frac {\cos(n\pi )}{n}}i={\frac {(-1)^{n}}{n}}i}$

für ${\displaystyle n\neq 0}$ und ${\displaystyle c_{0}=0}$, so dass zusammenfassend gilt:

${\displaystyle |c_{n}|^{2}={\begin{cases}{\dfrac {1}{n^{2}}},&{\text{falls}}\,\,n\neq 0,\\0,&{\text{falls}}\,\,n=0,\end{cases}}}$

und

${\displaystyle \sum _{n=-\infty }^{\infty }|c_{n}|^{2}=2\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }x^{2}\,\mathrm {d} x.}$

Damit ergibt sich die Lösung des Basler Problems:

${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {1}{4\pi }}\int _{-\pi }^{\pi }x^{2}\,\mathrm {d} x={\frac {\pi ^{2}}{6}}.}$

Ein weiterer Beweis ergibt sich aus der Berechnung der Fourierreihe für ${\displaystyle f(x)=x(1-x)}$:

${\displaystyle x(1-x)={\frac {1}{6}}-\sum _{n=1}^{\infty }{\frac {\cos(2\pi nx)}{{\pi }^{2}n^{2}}}}$

Die Lösung des Basler Problems ergibt sich, wenn man ${\displaystyle x=0}$ setzt.^[21]

Ein weiterer Beweis über Fourierreihen der Form ${\displaystyle \textstyle \sum _{n\not =0}{\frac {\cos(nx)}{n^{2}}}}$ findet sich in einem Buch von Fridtjof Toenniessen.^[22][23]

Verallgemeinerungen

Auch verallgemeinerte Euler das Problem. Er untersuchte dafür die später riemannsche ζ-Funktion genannte Funktion

${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+{\frac {1}{4^{s}}}+\cdots }$

und fand einen allgemeinen geschlossenen Ausdruck für alle geradzahligen natürlichen Argumente ${\displaystyle s=2k}$, nämlich

${\displaystyle \zeta (2k)=(-1)^{k-1}{\frac {(2\pi )^{2k}}{2(2k)!}}B_{2k}}$

wobei ${\displaystyle B_{2k}}$ die ${\displaystyle 2k}$-te Bernoulli-Zahl darstellt. Zur Ermittlung der Zeta-Funktionswerte von geraden Zahlen dient auch folgende Formel:

${\displaystyle \zeta (2k+2)={\frac {2}{2k+3}}\sum _{n=1}^{k}\zeta (2n)\zeta (2k+2-2n)}$

Dabei ist ${\displaystyle k\in \mathbb {N} }$. Eine allgemeine Formel für ungeradzahlige natürliche Argumente ${\displaystyle s}$ (siehe z. B. Apéry-Konstante) ist bisher unbekannt. Die Erweiterung auf reziproke Kuben hatte schon Euler versucht.^[24]

Literatur

• Lawrence Downey, Boon W. Ong, James A. Sellers: Beyond the Basel Problem. Sums of Reciprocals of Figurate Numbers. In: The College Mathematics Journal. Band 39, Nr. 5, November 2008, S. 391–394 (englisch). 
• C. Edward Sandifer: Euler’s solution of the Basel problem—the longer story. In: Robert E. Bradley (Hrsg.): Euler at 300 (= The MAA tercentenary Euler celebration. Spectrum series. Band 5). Mathematical Association of America, Washington DC 2007, ISBN 978-0-88385-565-2, S. 105–117 (englisch). 
• Martin Aigner, Günter M. Ziegler: Das Buch der Beweise. Springer, 2018.

Weblinks

• Leonhard Euler: De Summis Serierum Reciprocarum (lateinisch, englisch), englische Übersetzung bei Arxiv (Eulers erster Beweis, Euler-Verzeichnis E 41)
• Wie Euler einmal pfuschte: Das Basler Problem von Edmund Weitz
• Evaluating ζ(2) – 14 Beweise für den Wert von ζ(2) zusammengestellt von Robin Chapman auf einer Webseite der University of Exeter (engl.; PDF, 181 kB)
• The Inverse Pythagoras Theorem (Video englisch, Untertitel deutsch)

Einzelnachweise

1. ↑ Euler, De summis serierum reciprocarum, Opera Omnia,Reihe I, Band 14, S. 73–86, in der Standard-Notation der Werke von Euler von Eneström ist das E 41, zuerst erschienen in Comm. Acad. Petrop. 7 (1734/35), St. Petersburg 1740, S. 123–134. Die Arbeit wurde im Dezember 1735 der Akademie vorgelegt.
2. ↑ Dunham, Euler, the master of us all, MAA, S. XXII
3. ↑ Eine Liste gibt André Weil, Number Theory from Hammurabi to Legendre, Birkhäuser 1984, S. 262, darunter Daniel und Johann Bernoulli, James Stirling, Abraham de Moivre. Euler kündigte das Ergebnis in einem Brief im Dezember 1735 an. Der Brief ist in Euler, Opera Omnia, Reihe III, Band 2, S. 73–74, teilweise übersetzt in Calinger, Euler, S. 119, Weil, Number Theory from Hammurabi to Legendre, S. 261
4. ↑ Calinger, Leonhard Euler, Princeton UP 2016, S. 119
5. ↑ Euler, Demonstration de la somme de cette suite 1+1/4 + 1/9 +1/16 + 1/25 + 1/36 + etc., Opera Omnia, Reihe I, Band 14, S. 177–186, in der Standardnotation der Werke E 63, zuerst erschienen in Journal littéraire d' Allemagne, de Suisse et du Nord, Band 2:1, Den Haag 1743, S. 115–127
6. ↑ Martin Aigner, Günter M. Ziegler: Das Buch der Beweise, Springer 2018, S. 61–72
7. ↑ LeVeque, Topics in Number Theory, Band 1, Addison-Wesley, 1956
8. ↑ Robin Chapman, Evaluating ${\displaystyle \zeta (2)}$, Beweis 13, siehe Weblinks
9. ↑ A. M. Yaglom, I. M. Yaglom, Challenging mathematical problems with elementary solutions, Band 2, Holden-Day 1967
10. ↑ Beukers, Kolk, Calabi, Sums of generalized harmonic series and volumes, Nieuw Archief voor Wiskunde, Band 11, 1993, S. 217–224
11. ↑ Robin Chapman, Evaluating ${\displaystyle \zeta (2)}$, Beweis 2, siehe Weblinks
12. ↑ Robin Chapman, Evaluating ${\displaystyle \zeta (2)}$, Beweis 8, siehe Weblinks
13. ↑ Aigner, Ziegler, Das Buch der Beweise, Springer 2018, S. 210ff
14. ↑ Euler, Institutiones calculi differentialis cum ejus usu in analysi infinitorum ac doctrina serierum, St. Petersburg 1755, Opera Omnia, Reihe I, Band 10
15. ↑ Siehe z. B. C. J. Sangwin: An infinite series of Surprises, Euler`s Solution of the Basel problem, Plus Magazine
16. ↑ M. Bischoff: Pi ist überall – Teil 3.1: Was ergibt 1 + 1/4 + 1/9 + 1/16 + …? Spektrum.de, 3. Juni 2022, abgerufen am 19. Juni 2022. 
17. ↑ Reimund Albers: Das Baseler Problem. (pdf) Eine geometrische Lösung 2. Vorbereitung. Universität Bremen, abgerufen am 19. Juni 2022. 
18. ↑ Johan Wästlund: Summing inverse squares by euclidean geometry. (pdf) Abgerufen am 19. Juni 2022 (englisch). 
19. ↑ Adela Carmen Novac: A new solution to Basel problem, Annals of the Tiberiu Popoviciu Seminar, Vol. 15, 2017, 37–40.
20. ↑ James D.Harper, Another simple proof of ${\displaystyle 1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}}$, American Mathematical Monthly, Band 110, Nr. 6, 2003, S. 540–541
21. ↑ Robin Chapman, Evaluating ${\displaystyle \zeta (2)}$, Beweis 5, siehe Weblinks
22. ↑ Fridtjof Toenniessen, Das Geheimnis der transzendenten Zahlen Springer 2019, S. 331–333
23. ↑ Er entspricht Beweis 6 in Robin Chapman, Evaluating ${\displaystyle \zeta (2)}$, siehe Weblinks
24. ↑ William Dunham, Euler and the Cubic Basel Problem, American Mathematical Monthly, Band 128, 2021, Nr. 4